Développement limité h(x) = f(x)^2

[novicemaths]

Bonsoir

On me donne

Je cherche

J'ai tout bêtement fait , je sais que c'est faux.

Est-ce qu'il ne faudrait pas utiliser une formule de type binôme de Newton pour répondre à cette exercice.

A bientôt

[WillyCagnes]

bjr
tu as oublié les produits intermédiaires
developpe simplement (a+b+c+d+e)²

[(a+b) +(c+d+e)]² plus simple encore à developper de la forme (x+y)²

[novicemaths]

Merci WillyCagnes !!

Que je suis stupide f(x)² = f(x)*f(x)

A bientôt

[tournesol]

On a
tu ne conserves que les produits d'ordre inférieurs à 4 :

j'ai écris "petit o" car
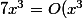Si je tiens ton énoncé pour vrai alors
On a alors
Rappel:
L'autre inclusion est fausse: mais