Je sèche sur la fin de ce problème.
En effet, j'ai trouvé la conjecture qui est a priori 1/2 mais sachant que la somme des carrés blancs est différente selon que n soit pair ou impair, je n1arrive pas á la démontrer...
Je vous remercie d'un petit coup de main éventuel....
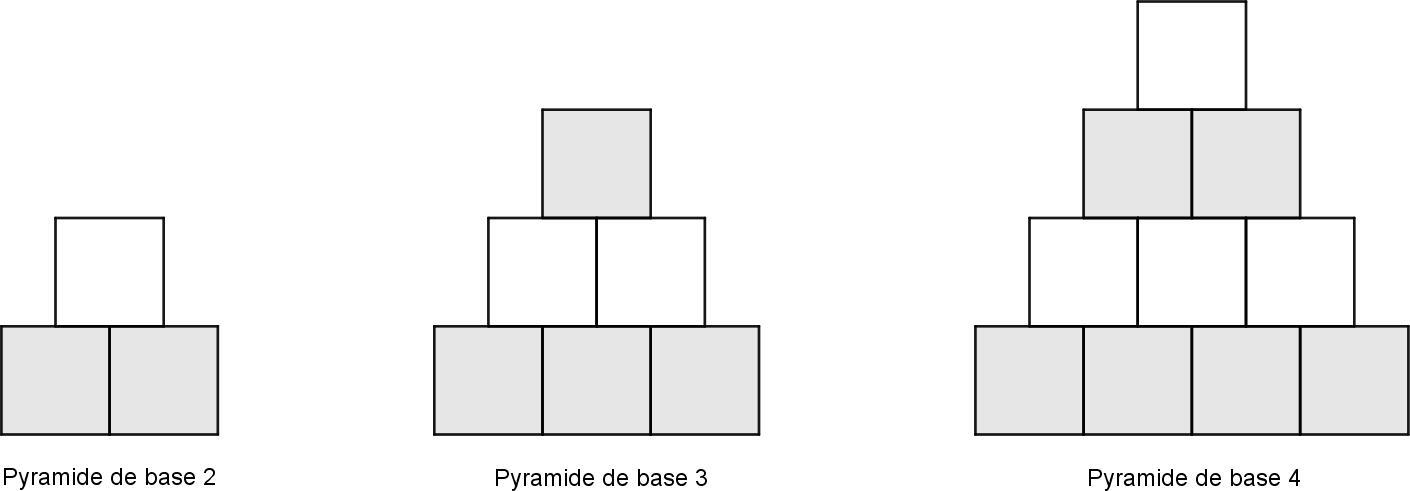
1. Construire et colorier les pyramides de bases 5, 6 et 7 comme celles de l’énoncé.
2. Pour chacune des pyramides de base 2, 3, 4, 5, 6 et 7, calculer la proportion de carrés blancs, c’est-à-dire la fraction de carrés de la pyramide qui ne sont pas coloriés. Que constate-t-on ?
3. Que peut-on conjecturer concernant les proportions de carrés blancs de la pyramide de base 25 ?
4. Étude d’un cas particulier
a. De combien de carrés est formée la pyramide de base 60 ?
b. Combien de carrés blancs comporte-t-elle ?
c. Quelle est la proportion de carrés blancs de cette pyramide ?
5. Recopier et compléter la conjecture suivante : « Plus on augmente le nombre de carrés de la base, plus la proportion de carrés blancs s’approche de … ».
6. Soit n un entier naturel supérieur à 1. Exprimer, en fonction de n,
a. le nombre de carrés qui forment la pyramide de base n,
b. le nombre de carré blancs de cette pyramide,
c. la proportion de carrés blancs de la pyramide de base n.
7. Démontrer alors la conjecture du 5.