Bonjour, je travaille un exercice dont le but est d'étudier cette fonction.
Soit donc la suite de fonction
)
définie pour
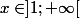
par:
=\dfrac{1}{n^x})
.
La fonction Zeta, est définie sur
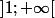
par:
=\sum\limits_{n=1}^{+\infty} f_n(x))
.
Le but de la question est de prouver que la limite, en

, de
)
est 1.
Pour cela, j'ai déjà montré que la série
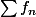
converge uniformément sur
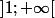
et que la limite de
)
vaut 1 si n=1 et 0 si
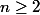
.
A partir de ces ingrédients, il nous faut donc prouver que la limite en

de
)
vaut 1.
Je pars ainsi:
=\sum\limits_{n=1}^{+\infty} f_n(x)=f_1(x)+ \sum\limits_{n=2}^{+\infty} f_n(x))
.
Le premier terme de cette somme a pour limite 1. Il me faudrait prouver que le second terme a pour limite 0 pour conclure. L'aide du manuel nous invite à utiliser la convergence uniforme... Tout ce que j'arrive à en conclure selon le cours, c'est que la somme
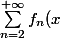)
est une fonction continue car limite uniforme d'une série de fcts continues. Mais à part dire cela, je ne sais pas trop quoi faire... Je concois bien que chaque chacun des termes de cette somme a une limite nulle, néanmoins, je reste prudent pour la conclusion car il s'agit d'une somme infinie et je suppose qu'il faut un vrai argument pour conclure, autre que 0+0+0+....=0 !
Merci pour votre aide, bonne journée à tous

