Action de groupe par translation à gauche

[PythagoreSauvage]

Bonjour à tous, ya-t-il un moyen de caractériser les stabilisateurs pour l'action par translation à gauche de sur : ?

On sait que pour ,

J'aurais envie de dire déjà mais est-ce la seule ?

[tournesol]

0

[tournesol]

si P et Q stabilisent M , disons à gauche , alors il en est de même de ,PQ , et QP .
Stab(M) est un sous groupe de GLn(K).
Mais ça ne répond pas à la question .
Si rang(M)=n , c'est Id.Dans le cas contraire, je ne pense pas.
Ce qui est facile à voir , c'est que P stabilise M à gauche ssi les colonnes de M sont des vecteurs propres de P associés à la valeur propre 1.

[tournesol]

Il s'agit des marices d'isomorphismes qui laissent invariant vect(colonnes(M))

[GaBuZoMeu]

Bonjour,

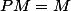
si et seulement si est l'identité sur l'image de .
Si on fait un changement de base en complétant une base de l'image de , on peut se faire une idée assez claire du stabilisateur de . On voit qu'il est isomorphe au produit semi-direct , où est le rang de .

[tournesol]

Merci beaucoup GaBuZoMeu.
Des révisions d'algèbre en perspective(produit semi-direct).