Exercice de récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 21 Fév 2023, 14:27
par scaar67 » 21 Fév 2023, 14:27
Bonjour je n'arrive pas a faire un exercice de récurrence voila l'énonce
In=
^n})
Exprimer In+1 en fonction de In, pour tout n ∈ N^*
j'ai essayer de poser In+1 et essayer de bidouiller l'expression mais je n'arrive pas a trouver le bon chemin est ce que vous auriez des pistes
je vous remercie d'avance
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Fév 2023, 15:15
par GaBuZoMeu » 21 Fév 2023, 15:15
Bonjour,
C'est avant tout un exercice d'intégration par parties. Tu as d'ailleurs mal écrit ton intégrale, tu as oublié le
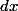
.
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 21 Fév 2023, 18:08
par scaar67 » 21 Fév 2023, 18:08
merci pour votre réponse
j'ai essaye de faire l'IPP mais je ne vois pas ou ca mène:
voila ce que j'ai fait
/(x^2+1)^n}dx=1/(x^2+1)^n-\int_{0}^{1}{-2nx(x^2+1)^{-n-1}}xdx)
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 22 Fév 2023, 11:54
par catamat » 22 Fév 2023, 11:54
Le résultat est faux, il manque des x...
Rappel:
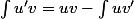
Que vaut u(x) ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2023, 12:08
par GaBuZoMeu » 22 Fév 2023, 12:08
Une partie est correcte, l'autre ne va pas du tout. Déjà, parce qu'il y a un

qui est une variable libre et pas une variable d'intégration, alors que ce que tu manipules est une intégrale définie (constante, ne dépendant pas de

). Ensuite effectivement, il faut faire plus attention dans l'application de la formule d'IPP.
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 22 Fév 2023, 14:14
par catamat » 22 Fév 2023, 14:14
Ok Gabuzomeu j'étais intervenu un peu rapidement...

Une astuce pour continuer à la place de x² écrire x²+1-1 ce qui est la même chose mais cela permet de faire apparaître
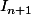
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 22 Fév 2023, 19:21
par scaar67 » 22 Fév 2023, 19:21
merci pour vos réponses je vais essayer de refaire l'IPP proprement
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 22 Fév 2023, 20:08
par scaar67 » 22 Fév 2023, 20:08
voici ce que j'ai poser pour l'IPP
u(x)=
^n})
v'(x)=1
ainsi u'(x)=
^{-n-1})
(j'espère que je me suis pas trompe)
et v(x)=x
puis je fais l'IPP je n'ai pas mis les bornes encore pour voir plus clair :
et je trouve ca
^n}-\int -2nx(x^2+1)^{-n-1}xdx)
est ce que c'est juste ? jusqu'à la ?
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 22 Fév 2023, 20:12
par scaar67 » 22 Fév 2023, 20:12
est ce que je dois maintenant intégrer ?
^{-n-1}xdx)
ou y a une technique pour faire apparaitre le In+1 ?
-
scaar67
- Messages: 6
- Enregistré le: 21 Fév 2023, 14:21
-
 par scaar67 » 22 Fév 2023, 20:55
par scaar67 » 22 Fév 2023, 20:55
scaar67 a écrit:est ce que je dois maintenant intégrer ?
^{-n-1}xdx)
ou y a une technique pour faire apparaitre le In+1 ?
ooh non j'ai n'importe quoi dans mes précédents messages je crois que j'ai compris enfaite faut que j'utilise les bornes
on a
^n}-\int_{0}^{1}{-2nx(x^2+1)^{-n-1}x}dx)
=
^n}-\int_{0}^{1}{\frac{-2nx^2}{(x^2+1)^{n+1}}})
=
^n}+2n\int_{0}^{1}{\frac{x^2}{(x^+1)^{n+1}}}dx)
=
^n}+2n\int_{0}^{1}{\frac{x^2+1-1}{(x^2+1)^{n+1}}}dx)
=
^n}+2n\int_{0}^{1}{\frac{x^2+1}{(x^+1)^{n+1}}-\frac{1}{(x^2+1)^{n+1}}}dx)
j'applique les bornes sur
^n})
ce qui nous fait
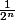
Donc In+1=
a la fin l'expression ressemble a
)
donc
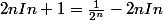
La je pense que j'ai fini l'exercice
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 22 Fév 2023, 21:59
par GaBuZoMeu » 22 Fév 2023, 21:59
Tes égalités sont incorrectes si tu n'appliques pas les bornes dès le début !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
ou y a une technique pour faire apparaitre le In+1 ?