Bonjour tout le monde!
J'étudie présentement le nombre N=51^122 - 7^235 et je cherche à trouver il y a combien de puissances de 2, de 3, de 5 et de 7 lorsqu'on développe N en facteurs premiers.
Pour l'instant, je sais qu'il y a 0 puissance de 5 puisque j'ai trouvé que N est congrue à 58 (mod 100). Ensuite, j'ai trouvé que 51^122 > 7^235 car 7^235 = 49^122 * 7/49^5.
Développement en facteurs premiers d'un très grand nombre
10 messages
- Page 1 sur 1
Re: développement en facteurs premiers d'un très grand nombr
Tu as trouvé que ce nombre est congru à 58 modulo 100. Je n'ai pas vérifié. Si ce calcul est bon, ceci répond à 2 de tes questions.
Et pour les 2 autres questions, il n'y a aucun calcul à faire, la réponse est immédiate.
Et pour les 2 autres questions, il n'y a aucun calcul à faire, la réponse est immédiate.
Re: développement en facteurs premiers d'un très grand nombr
Bonjour
La congruence est juste :
51² = 1[100]
donc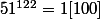
d'autre part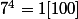 donc
donc 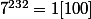 et
et 
donc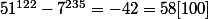
La congruence est juste :
51² = 1[100]
donc
d'autre part
donc
Re: développement en facteurs premiers d'un très grand nombr
Bonjour,
Merci pour vos réponses, mais je ne comprends pas comment le fait de savoir que les deux derniers chiffres sont 58 peuvent m'aider à connaître le nombre de puissances de 2, de 3 et de 7 dans N? Je sais que ma congruence est juste, mais je n'arrive pas à répondre à la question.
Merci pour vos réponses, mais je ne comprends pas comment le fait de savoir que les deux derniers chiffres sont 58 peuvent m'aider à connaître le nombre de puissances de 2, de 3 et de 7 dans N? Je sais que ma congruence est juste, mais je n'arrive pas à répondre à la question.
Re: développement en facteurs premiers d'un très grand nombr
Le 58 te permet de répondre à la question 'combien de 5', ok; il te permet aussi de répondre à la question 'combien de 2'.
Les 2 autres questions sont beaucoup plus simples. Là, tu as calculé ce 58 qui est un calcul compliqué. Pour les 2 autres questions, il n'y a aucun calcul à faire. Juste une particularité à observer.
Dans l'ordre, du plus simple au plus compliqué, l'exercice pourrait être formulé ainsi
Combien de 7
Combien de 3
Combien de 5
Combien de 2.
Les 2 autres questions sont beaucoup plus simples. Là, tu as calculé ce 58 qui est un calcul compliqué. Pour les 2 autres questions, il n'y a aucun calcul à faire. Juste une particularité à observer.
Dans l'ordre, du plus simple au plus compliqué, l'exercice pourrait être formulé ainsi
Combien de 7
Combien de 3
Combien de 5
Combien de 2.
Re: développement en facteurs premiers d'un très grand nombr
Ok, mais dans le fond je sais qu'il y a un x nombre de puissances de 2, mais comment je fais pour trouver ce x?
Re: développement en facteurs premiers d'un très grand nombr
Commence par les questions que j'ai mis au début. Ce sont les plus simples. Et tu peux aussi réfléchir. Ces exercices sont faits pour ça, pour te faire réfléchir. Pas pour que tu demandes la réponse toute faite.
Re: développement en facteurs premiers d'un très grand nombr
p premier.Combien de p dans n?
l'unique k tel que (n congru à 0 modulo p^k)et(n non congru à 0 modulo p^(k+1))
Pour 2 , k est supérieur ou égal à 1 car la différence de deux impairs est paire.
ton nombre est congru à (1)^122-(-1)^235, donc à 2 modulo 4
donc k(2)=1
A toi pour la suite.
l'unique k tel que (n congru à 0 modulo p^k)et(n non congru à 0 modulo p^(k+1))
Pour 2 , k est supérieur ou égal à 1 car la différence de deux impairs est paire.
ton nombre est congru à (1)^122-(-1)^235, donc à 2 modulo 4
donc k(2)=1
A toi pour la suite.
Modifié en dernier par tournesol le 14 Fév 2023, 20:50, modifié 2 fois.
Re: développement en facteurs premiers d'un très grand nombr
Bonjour Tournesol
Es tu sûr qu'un nombre congru à 58 modulo 100 soit divisible par 4 ??
Es tu sûr qu'un nombre congru à 58 modulo 100 soit divisible par 4 ??
Re: développement en facteurs premiers d'un très grand nombr
Merci catamat.
C'est moi qui devrais m'appeler catamat.
J'ai modifié mon message.
C'est moi qui devrais m'appeler catamat.
J'ai modifié mon message.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
