Idéal engendré par une réunion

[PythagoreSauvage]

Salut à tous, j'ai un petit résultat à montrer. Le voici :

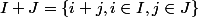
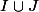
Soit un anneau commutatif. Soient , deux idéaux de . On montre aisément que l'ensemble est un idéal de . Je dois maintenant montrer que c'est l'idéal engendré par . Pour rappel, l'idéal engendré par une partie de c'est le plus petit idéal de qui contient cette partie . On le note et il est obtenu en faisant l'intersection de tous les idéaux de qui contiennent .

Je dois donc montrer la chose suivante :

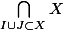
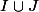
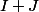
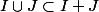
Je pensais procéder par double inclusion. Par définition, est le plus petit (au sens de l'inclusion) idéal qui contient . Or est un idéal de et donc nécessairement .

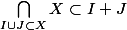
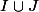
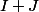
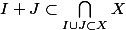
J'aimerai maintenant montrer l'inclusion inverse. Je dois donc montrer que pour toute idéal de , si contient alors il contient aussi donc on aurait . Mais là je ne vois pas.

Merci pour votre aide

[GaBuZoMeu]

Bonjour,
Vu que tu sais déjà que est un idéal qui contient et , il te suffit de montrer que tout idéal qui contient et (c.à-d. qui contient ) contient .
Tu prends donc un élément de , un élément de , et tu te demandes si un idéal qui contient et contient forcément ...

[PythagoreSauvage]

Ah bah oui ça devient évident. Soit idéal de tel que . On a en particulier et . Il existe tels que et

Et comme est un sous-groupe de , est encore dans . Conclusion, tout idéal qui contient contient aussi .
Donc

Par conséquent

[PythagoreSauvage]

Merci beaucoup pour l'aide !

[GaBuZoMeu]

Sauf que ton argument ne va pas : tu fais un gros contresens sur l'usage des quantificateurs.
Ce qu'il faut montrer c'est que POUR TOUT et POUr TOUT , .
Or ce que tu écris c'est "Il existe "