Fonction racine xième de x
Olympiades mathématiques, énigmes et défis
-
Thiéfaine
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Oct 2022, 19:19
-
 par Thiéfaine » 06 Jan 2023, 12:11
par Thiéfaine » 06 Jan 2023, 12:11

J'ai regardé des vidéos sur la dérivée de
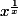
.
Mais savoir que cette fonction croît jusqu'en (e; e^(1/e)), son maximum, puis décroît n'est pas ce qu'il me faut..

Et puis il y a un sûrement, comme d'habitude, un chemin beaucoup plus facile et rapide.
Une piste ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Jan 2023, 13:06
par Doraki » 06 Jan 2023, 13:06
Eh bien x -> x^60 est croissante donc tu pourrais simplement comparer leurs puissances 60ème, qui vont tous être des entiers.
-
Thiéfaine
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Oct 2022, 19:19
-
 par Thiéfaine » 06 Jan 2023, 13:15
par Thiéfaine » 06 Jan 2023, 13:15
Merci !
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 06 Jan 2023, 14:32
par catamat » 06 Jan 2023, 14:32
Bonjour
On n'a pas besoin d'aller jusqu'à 60 si on a la dérivée, puisque le maximum est atteint pour e, la plus grande valeur est atteinte pour x égal à 2 ou 3.
Donc on élève à la puissance 6,
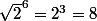
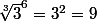
Comme 8<9 le nombre le plus grand est
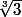
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités

