Série entière

[linkereover]

Bonjour,
Soit , où est telle que .
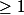
On sait que le rayon de convergence est , et donc que est holomorphe sur .
Mais commet justifier que est continue sur ? J'imagine qu'il doit y avoir le théorème d'Abel derrière cela, mais je ne vois pas trop comment l'utiliser.... (la version radiale ne donne la continuité que dans un "cône"....)
Merci d'avance pour votre aide !

[GaBuZoMeu]

Bonjour,

On a donc, d'après l'hypothèse, convergence normale de la série sur le disque unité fermé.

[linkereover]

Effectivement... merci beaucoup !
Je cherchais compliqué alors que la réponse était juste sous mon nez...

[GaBuZoMeu]

Avec plaisir.