LOI NORMALE

[mathdestructor]

Bonjour,
Je voudrais comprendre pourquoi dans un diapo ont nous présente une loi normale avec ( 1-Valueur tableau de fonction de répartition ) et un autre coup il prend QUE le résultat dans la table de répartition alors QUE C'EST EXACTEMENT LA MEME SITUATION
Merci d'avance

[mathdestructor]

Je viens de remarquer un truc, POURQUOI P(Z égale ou supérieur 0,5) devient P( Z égale ou inférieur )... J'en ai marre xd

[phyelec]

Bonjour,

Un petit rappel de cours sur la fonction de répartition d'une variable aléatoire continue X ,vous permettra sans doute de vous y retrouver .

la fonction de répartition définie par : F(x) = P[X ≤ x] = P[X < x].
On a les propriétés suivantes :
1) F est une continue,
2) lim x→−∞ F(x) = 0 et lim x→+∞ F(x) = 1,
3) F est une fonction croissante,
4) Pour tous a, b ∈ R et a < b, F(b) − F(a) = P[a < X ≤ b]

[phyelec]

un petit exemple :

P(2 ≤ X ≤ 11) =F(11)-F(2)= P(X ≤ 11)− P(X ≤ 2)

P(-2 ≤ X ≤ 11) =F(11)-F(-2)= P(X ≤ 11)− P(X ≤ -2) et F(-2)=1-F(2)=1-P(X ≤ 2)=P(X ≤ -2)

[mathdestructor]

un petit exemple :

P(2 ≤ X ≤ 11) =F(11)-F(2)= P(X ≤ 11)− P(X ≤ 2)

P(-2 ≤ X ≤ 11) =F(11)-F(-2)= P(X ≤ 11)− P(X ≤ -2) et F(-2)=1-F(2)=1-P(X ≤ 2)=P(X ≤ -2)

Je ne comprend toujours pas pourquoi P(2 ≤ X ) devient P(X ≤ 2)
C'est strictement l'inverse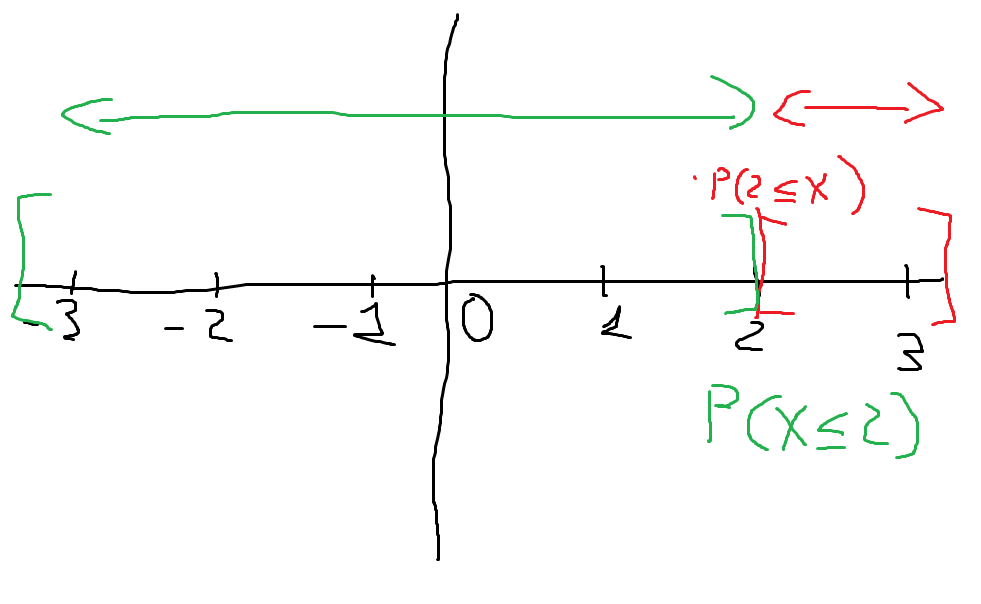

[phyelec]

Pourquoi dessinez-vous une droite ?, il s'agit de probabilité et de loi normale ( donc de loi gaussienne), ce n'est pas les mêmes règles qui s'appliquent.

Vous écrivez "Je ne comprend toujours pas pourquoi P(2 ≤ X ) devient P(X ≤ 2)", ce n'est pas ce qui est écrit.
Je tente de vous expliquer:
On applique la définition du point 4) Pour tous a, b ∈ R et a < b, F(b) − F(a) = P[a < X ≤ b] donc
F(11)-F(2)=P(2 ≤ X ≤ 11) puis on applique la définition de la fonction de répartition définie par : F(x) = P[X ≤ x] à F(11) et f(2) :
- pour F(11) on a x=11 donc F(x) = P[X ≤ x] devient F(11) = P[X ≤ 11]
- pour F(2) on a x=2 donc F(x) = P[X ≤ x] devient F(2) = P[X ≤ 2]
On n'a pas écrit que P[2 ≤ X] devient P[X ≤ 2] mais que P(2 ≤ X ≤ 11) =P[X ≤ 11]-P[X ≤ 2] le "P" de Probabilité change tout, vous regardez la probabilité dans un intervalle d'une gaussienne puisque vous êtes en loi normale, votre raisonnement sur une droite avec des nombres ne peut s'appliquer.

[GaBuZoMeu]

Bonjour,

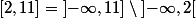
Pour parler avec des ensembles contenus dans la droite : (l'intervalle privé du sous intervalle ).

Avant de dire des bêtises sur ton prof, fais l'effort de bien comprendre ce qu'il écrit !