Résolution d'équation trigo

[Krampish]

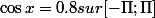
je trouve S= {arcos 0.8 +2k. ; - arcos 0.8 +2k.}




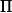
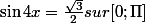
je trouve S= { ; }




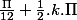
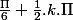
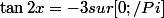
je trouve:


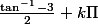
J'ai un doute concernant les intervalles donnés pour faire l'exercice. Y a t-il des valeurs trouvées qui ne fonctionnent pas vu l'intervalle donné?

Merci pour votre aide;

[catamat]

Bonjour

En effet il ne faut prendre que les solutions situés dans l'intervalle.

Pour la deuxième par exemple , c'est correct si l'on résout dans R mais là l'intervalle est de longueur un demi tour, or entre chaque solution il y a un quart de tour, on va donc trouver deux nombres pour chacune des deux solutions dans R.

pour x= Pi/12 + k Pi/2
Si k= 0 on a x=Pi/12 qui est dans [0;PI]
Si k=1 on a x=7Pi/12 qui est aussi dans [0;Pi]

Si k<0 ou k>1 , x n'est pas élément de [0;Pi] donc deux valeurs pour cette solution, idem pour l'autre

[Krampish]

Bonsoir,

Je viens de me rendre compte que dans l'énoncé je me suis trompé de ans l'intervalle donné qui est [pi/2, pi].

Je trouve donc les résultats suivant.

1. S ={arccos 0.8, - arccos 0.8}

2. S = {7pi/12, 2pi/3}

3. S= {(arctan - 3)/2}

Trouvez vous pareil que moi.

Cordialement

[catamat]

Ok pour les deux premiers en tenant compte du changement d'intervalle pour la 2e.

Mais pour la 3, arctan(-3) vaut environ -1.25 donc on est hors intervalle... (ajouter Pi)