Résoudre une inéquation

[wanamax]

Bonjour, j'aurais besoin d'aide pour résoudre l'inéquation suivante svp :

1/n ≥ ln(1+1/n)

Merci d'avance

[catamat]

Bonjour

Déterminer le signe de f(x)=ln(1+x)-x après avoir étudié ses variations.

[mathelot]

Bonjour,



f est concave , sa courbe est située sous ses tangentes
La tangente à la courbe du log en x=1 a pour équation y=x-1
donc
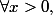ln(x)
posons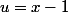
il vient:

[mathou13]

Bonjour,


1/n >=ln(1+1/n)
f(n)=ln(1+1/n)-1/n
f'(n)=(-1/n^2)/((n+1)/n)+1/n^2
f'(x)=-n/(n^2(n+1))+1/n^2
=(-n+n+1)/(n^2(n+1))
=1/(n^2(n+1))
_n___/-inf____-1___0_______+inf
f'(n)/______-___//_+__+______
f(n)/______

Comme lim(x->+inf) f(x)=0-
lim(x->-1+) f(x)=-Infini
La fonction x->f(x) réalisé une bijection de ]-1;+inf[ dans ]-infini;0-[ Donc 1/n>=ln(1+1/n) pour tous n>-1