Integrale généralisée

[tgaouss]

Bonjour tout le monde. Svp aidez moi avec cette question :
Etudier la convergence de l'intégrale ci-dessous :
Intégration de 0 à +Infini lnx/(x2 + 1)

[phyelec]

Bonsoir,

calculez cette intégrale par une intégration par partie (cela se fait très bien) et regardez.

[tgaouss]

Ok je vais essayer. Merci !

[mathelot]

Bonsoir,

calculez cette intégrale par une intégration par partie (cela se fait très bien) et regardez.

@phyelec : tu peux préciser, je ne vois pas ?

[phyelec]

j'ai compris hier soir que l'intégrale est : qui se fait par IPP.

par contre ce matin je me dis que c'est peut-être :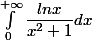 effectivement par IPP je ne vois pas . il faut séparer l'intégrale sur 2 intervalles ]0;1] et [1, et faire le changement de variable v=1/x sur l'intervalle ,

[tgaouss]

Ok bien reçu. Mais j'ai vu quelque part que cette intégrale était équivalente à :
Intégrale de 0 à +infini de (X exposant (3/2) x lnX) / (X2 + 1).
Pourriez vous m'expliquer cette expression. Je suis confus. Merci

[phyelec]

de quelle intégrale parlez-vous, celle que j'avais compris hier soir ou celle que je supposais ce matin.

[tgaouss]

il s'agit effectivement de celle de ce matin

[GaBuZoMeu]

Bonjour,
Vu les règles de priorité habituelle, la fonction qu'on intègre est , et il suffit de comparer à des avec bien choisi au voisinage de 0 et au voisinage de 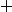pour avoir la réponse sur la convergence.

[tournesol]

la fonction est équivalente à ln x au voisinage de zéro, qui est constant au voisinage de zéro et qui se primitive en xln x-x , d'où la convergence en zéro.

[GaBuZoMeu]

"ln x ..., qui est constant au voisinage de zéro"
Qu'est-ce que tu racontes, tournesol ???

[mathelot]

il voulait dire "de signe constant"

[GaBuZoMeu]

Tu as vu ça dans ta boule de cristal ?

[tournesol]

Bien vu mathelot!
En +l'infini on a
Donc en +l'infini f(x) qui est positif est un