Forme exponentielle de nombre complexe

[Seldon²]

Bonjour une partie de mon dm de math expert me pose problème voici l'énoncé.
1.
a. Soit (1n) n ∈ N , la suite géométrique réelle de premier terme ro strictement positif et de raison 2/3. Exprimer rn, en fonction de ro et de n.

b. Soit (θn) n ∈ N , la suite arithmétique réelle de premier terme θo appartenant a l'intervalle [0. π/2] et de raison 2π/3. Exprimer θn, en fonction de θ0, et de n.

c. Pour tout entier naturel n, on pose Zn = rn(cosθn+ i sinθn) . Sachant que
Z0, Z1, et Z2 sont liés par la relation Z0Z1Z2 = 8, déterminer le module et un argument de Zo, Z1 et Z2

Pour la a j'ai trouvé rn = r0*2/3^n et pour la b θn = θ0+2π/3*n
Pour la c je bloque un peu :
j'ai mis Z0, Z1, et Z2 sous forme exponentielle pour simplifier les calculs donc
Z0 = r0*e^iθ0 = IZ1I*e^iθ0
Z1 = r1*e^iθ1 = IZ1I*e^iθ1
Z2 = r2*e^iθ2 = IZ2I*e^iθ2
On peut l'écrire sous cette forme car rn est strictement positif
D'après l'énoncé Z0Z1Z2 = 8 donc on peut remplacer par l'écriture exponentielle de Z0, Z1, et Z2
IZ1I*e^iθ0 * IZ1I*e^iθ1 * IZ2I*e^iθ2 = 8
IZ1I*IZ1I*IZ2I*e^iθ0*e^iθ1*e^iθ2=8
Sauf que je suis bloqué, je ne sais pas comment retrouvé les valeurs de r0 et de θ0 dont j'ai besoin pour trouver le module et un argument de Z0, Z1, et Z2

[lyceen95]

Tu as 3 complexes, dont le produit vaut 8

Donc le module de ce nombre complexe vaut 8, et son argument vaut 0.
Par ailleurs, l'énoncé n'es pas très clair, mais il faut certainement considérer que les hypothèses des questions a) et b) sont toujours valables.
Donc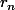 suit une suite géométrique de raison 2/3, et 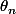suit une suite arithmétique de raison

[Seldon²]

J'ai essayé quelque chose et je trouve r0= 9 et θ0=0

Z1*Z1*Z2 = r0*r1*r2*e^iθ0*e^iθ1*e^iθ2
Z1*Z1*Z2 = r0*r0*2/3*r0*4/9*e^i(θ0+θ1+θ2)
Z1*Z1*Z2 = 3r0*8/27*e^i0 car il n'y a pas de partie immaginaire
8 = 3r0*8/27*1
r0 = 9/3*8/27 = 9

[lyceen95]

Non, il y a une erreur.

Z1*Z1*Z2 = r0*r0*2/3*r0*4/9*e^i(θ0+θ1+θ2)
Ok pour cette ligne.
Mais pas la ligne suivante.

[Seldon²]

c'est mieux si j'écris (r0)^3*8/27*e^i0

[lyceen95]

Quand on écrit un truc juste à la place d'un truc faux, oui, c'est mieux.