Différentiabilité

[Samoth]

Bonjour,

J'essaye d'étudier l'existence des dérivées partielles de l'application définie par en

Voilà ce que j'ai fait :

On a donc .

Bon, ça me paraît bizarre, puisque la valeur absolue n'est pas différentiable en ...

Qu'en pensez-vous ?

Merci !

[phyelec]

Bonjour,

Je pense qu'il faut étudier les 2 situations suivantes:
si x> 0 et y >0 si x< 0 et y <0 ou alors f(x,y)=xy
si x< 0 et y >0 ou si x>0 et y <0alors f(x,y)=-xy

[tournesol]

OK Samoth.
Ta méfiance t'honore mais il y a un produit de deux valeurs absolues.
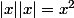
Ce n'est pas du aux deux variables car même avec la variable x on a qui est differentiable en zéro.

[Samoth]

Merci !
Finalement, pas d'inquiétude, car f est différentiable entout point de .

[tournesol]

f est differentiable en (0,0),sur le plan moins les axes, mais elle n'est pas differentiable sur les axes sauf en (0,0).
la dérivée partielle par rapport à y en (1,0) n'existe pas.

[Samoth]

Merci pour ta réponse tournesol.

Je m'intéresse maintenant à la continuité des dérivées partielles.
Regardons ce qu'il se passe en .
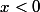
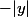
Pour la dérivée partielle en x, j'ai montré que si et si .
J'ai également montré en utilisant la définition de la dérivée partielle que .

J'ai envie d'en conclure que et donc que la dérivée partielle de f en x est continue en .

[tournesol]

la dérivée partielle en x n'existe pas sur l'axe des ordonnées sauf en (0;0)
Il en résulte que la dérivée partielle en x n'est pas définie au voisinage de (0;0)
Donc elle ne peut etre continue en (0;0)

[Samoth]

Je vois, merci.

Aurais-tu un exemple de fonction différentiable mais dont les dérivées partielles ne sont pas toutes continues ?

Je sais en effet que si f admet des dérivées partielles continues en tout point, alors f est différentiable.

Autre question : est-ce qu'on peut considérer la contraposée de cette affirmation, et dire que si f n'est pas différentiable, alors f n'admet pas de dérivées partielles ou f admet des dérivées partielles non continues ?

[tournesol]

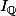
désigne la fonction indicatrice de
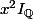
définit une fontion dérivable seulement en 0 .
Sur tu peux prendre qui ne sera dérivable qu'en (0;0).
tu as aussi
f(0)=0 et sinon f(x)=
dérivable sur R mais dérivée non continue en 0.

[Samoth]

Merci tournesol.

Je n'avais pas pensé à me ramener à R pour trouver un contre-exemple.
Merci pour les exemples !