Démonstration par récurrence d'une inégalité

[triumph59]

Bonsoir,

J'essaie de démontrer par récurrence l'inégalité suivante



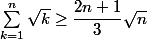
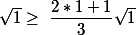
Pas de souci pour l'initialisation avec n=1 j'obtiens est vrai

Pour l'hérédité :
je calcule

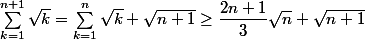
Je ne vois pas comment passer de n+1 à n+2 et faire apparaître le terme dans l'inégalité ?

Avez-vous une piste ?

[tournesol]

quand tu dis "une autre piste"
c'est pour une récurrence ou tu veux une autre méthode plus rapide(minoration par une intégrale facile)

[triumph59]

ça serait savoir si la récurrence est une piste valable ?

[lyceen95]

Quand on passe de n à n+1 , l'expression de gauche augmente de ... et celle de droite augmente de ...
Si on arrive à montrer que l'expression de gauche augmente plus que celle de droite, c'est gagné.
Et on y arrive.

[catamat]

Bonsoir

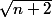
Le terme n'a pas lieu d'être !

[tournesol]

il te suffit de montrer que
Une soustraction suivie d'une élévation au carré règlent le pb.

[triumph59]

Bonsoir,

Je me suis pris la tête à chercher une solution trop compliquée
Merci pour vos réponses