Suite bornée

[LandAyZ]

Bonsoir,

J'ai un exercice en maths sur les suites où je bloque. Voici le sujet :
"soit (Un) une suite bornée telle que (Un-Un+1) soit croissante. Montrer que (Un) est croissante."

J'essaye de prouver que Un+1-Un > 0 mais difficile de conclure. Auriez-vous des pistes afin d'avancer ?
Merci d'avance.

[Kolis]

Un-Un+1=1 et je ne vois pas ce que cela apporte à Un.

Maintenant s'il s'agit de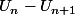 tu peux remarquer :
1. Cette suite croissante est elle aussi bornée
2. Que dire d'une suite monotone bornée ?
3. S'il y a une limite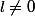 tu peux obtenir une contradiction.
4. Tout ça permet de conclure.

[LandAyZ]

Merci de votre réponse et désolé de répondre si tard.
Alors on sait que tend vers une limite l.
Maintenant il reste à prouver que l=0 pour avoir le résultat voulu.
J'arrive à une inégalité :

Je pense pouvoir l'utiliser pour aboutir à une contradiction en tendant n vers l'infini sauf qu'on ne sait pas si la suite Un converge donc je bloque

[tournesol]

Ton inégalité est fausse
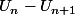est croissante donc cette difference est inferieure à l
Donc
Si l<0 , contradiction car est majorée .
Donc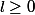
Si l>0 à partir d'un certain rang
Donc la suite est décroissante à partir d'un certain rang , et comme elle est bornée ...

[LandAyZ]

On a (Un) qui tend vers sa borne inf vu qu'elle est décroissante et minorée apcr. Ainsi tend vers 0. Or l>0 donc il ya contradiction. Donc l=0
Est-ce bien cela ?

[lyceen95]

J'ai des doutes sur ce que Tournesol a proposé.

Pour le point 3 du plan proposé par Kolis
Si la suite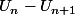 a une limite non nulle, alors on peut introduire le nombre ( ou n'importe quel autre nombre entre et ).
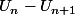A partir de certaines valeurs de , tous les termes sont plus grands en valeur absolue que ce , et tous de même signe, et là, on peut dire qu'il y a contradiction avec le caractère borné de notre suite.

[tournesol]

Je suis d'accord avec LandAyZ .
lyceen95 quels doutes as-tu?
lyceen95 ce que tu proposes doit être rédigé pour être convaincant .