Existence d'une fonction

[Capss]

Halo tout le monde!

Je coince sur une question d'un DM. C'est le suivant (je résume):

On a une région notée R de forme triangulaire et trois villes V1, V2 et V3 qui sont situées sur les sommets de coordonnées (x1,y1), (x2,y2), (x3,y3).

On a un répère identifié à R² et on considère T0, un triangle de référence O(0,0) I(1,0) J(0,1) et le but c'est de trouver une formule de changement de repère permettant de ramener la région R au triangle T0. Les variables parcourant T0 sont notées (u,v).
Connaissant les coord de chaque ville(xi,yi), il faut donc trouver l'expression d'un difféomorphisme f: R²->R² envoyant To sur R.

Voici la question sur laquelle je bloque:
1* Justifier sans calcul, l'existence et l'unicité d'une fonction f:R²->R² dont les composantes sont des fonctions polynômes du 1er degrè en x et y t.q. f(O)=V1, f(I)=V2 et f(J)=V3.
2* Montrer qu'elle est bijective

J'ai pensé à dire que tout point par f donne une nouvelle direction. 3 points par f donne alors 3 points de l'espace et si ces points ne sont pas alignés, alors passe un unique plan. Mais ce raisonnement n'est pas correct car ici c'est pas f: R²->R mais R²->R² :hein:
Ensuite pour la bijectivité je ne vois pas :triste:

Merci d'avance à celui qui pourra m'aider :happy2:

[mathelot]

l'existence et l'unicité de la fonction cherchée de dans
sont données par la géométrie affine.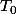 et sont deux repères affines du plan et il existe donc une unique application affine bijective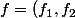
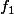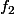de dans qui envoie un repère sur l'autre. Les applications coordonnées et sont des application affines de dans soit de la forme:

La bijection réciproque de f, notée g, de dans envoie le deuxième repère sur le premier.

[mathelot]

la deuxième coordonnées de f est de la forme:

l'application linéaire associée à l'application affine envoie la base sur la base ,
est bijective car est bijective.

[Capss]

merci de ta réponse mathelot! Vais essayer de comprendre tout ça :we:

Bonne année.

[Capss]

Ensuite dans la suite de l'énoncé, on définie une fonction comme tu as défini.

Fi : R²-> R²
les cstes sont des réels
et on demande de montrer que pour G=bar(M1(x1,y1)/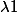......Mn(xn,yn)/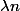) avec M1(x1,y1)....Mn(xn,yn) n points du plan et 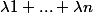, Fi(G)=bar [phi(M1)/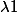......phi(Mn)/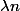] ça c'est bon. Puis vient la question en déduire que f (la fonction de la première question) transforme l'intérieur de T0 en l'intérieur de R et l'extérieur de T0 en l'extérieur de R. Déterminer f en fonction de (xi,yi) des points Vi (i appartenant à 1...3)
Je vois pas trop le lien avec la question sur le barycentre :hein:

Merci d'avance de vos lumières :marteau:

[mathelot]

je crois me rappeler que si 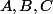est un triangle non aplati, son intérieur coïncide avec l'ensemble des points dont les coordonées barycentriques
normalisées (de somme égales à 1) sont toutes les trois strictement positives.
étant une application affine, elle conserve le barycentre, i.e, si M est barycentre de 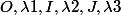, alors est barycentre
de affectés des mêmes coefficients. Donc envoie l'intérieur de 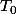sur l'intérieur de , bijectivement en plus.

[Capss]

Hello merci de la réponse
Sinon pour en revenir au premier post, comment je pourrais mq pour 2 repères affines, il existe une unique ap affine bijective de R² dans R² envoyant un repère sur l'autre? J'ai regardé dans des cours sur ce chapitre et j'ai pas trouvé cette proposition.

merci

[mathelot]

Deux repères affines ont le même nombre de points. Si 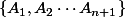et
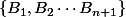
sont deux tels repères, si f envoie les points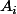 sur les points 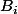pour 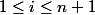, ta question est équivalente à montrer qu'il existe une unique application linéaire bijective 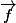qui envoie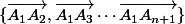
sur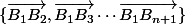 ce qui est le cas, car ces deux familles de vecteurs sont des bases.

[Capss]

merci bien :happy2:

[mathelot]

c'est le caractère affine de l'application qui permet de passer des points et d'un barycentre de ces points à une application linéaire et une combinaison linéaire de vecteurs ... et réciproquement.