Bijection sous condition (produit scalaire)

[Albator1902]

Bonjour, je vous fais part d’un exercice qu’un collègue m’a envoyé :

On considère un endomorphisme de E (espace vectoriel) f : x |—> x - <a,x>b
Avec a,b deux vecteurs non nuls de E et <.,.> un produit scalaire.
Il faut montrer que f est bijective si et seulement si <a,b> est différent de 1.

J’ai une belle démonstration dans le cas du produit scalaire canonique (par équivalence en utilisant la matrice canoniquement associée à f), mais je bloque quant à une généralisation à un produit scalaire quelconque.
Auriez-vous des pistes ? Ou est-ce simplement une imprécision de l’énoncé ?
Merci

[Rdvn]

Bonjour
Êtes vous toujours à la recherche d'une solution ?
J'en ai une ...
(je n'avais pas eu le temps de chercher jusqu' aujourd’hui,
il est difficile de vous retrouver parmi les spam imbéciles qui polluent le site malgré
le dévouement et les efforts des modérateurs)

[Rdvn]

Je fais "remonter" un peu à cause des spam

[tournesol]

Il est facile de montrer que ker(f) est nul ssi a.b différent de 1 .
Est on en dimension finie?

[Rdvn]

Bonjour à tous
@tournesol
c'était aussi le début de ma solution,
c'est donc terminé si E est de dimension finie.
Sinon on peut fixer y vecteur quelconque de E et remarquer que
H=Vect(y,a,b) est stable par f,
on peut donc considérer g, l’endomorphisme de H induit par f,
et conclure car H est de dimension finie
Bonne soirée

[tournesol]

Joli Rdvn !

[catamat]

Bonjour Rdvn,

Je pose cette question sans malice juste pour comprendre.

Pourquoi faire intervenir y ? Pourquoi ne peut on pas utiliser H=Vect(a,b) qui est stable par f ?

Merci

[Rdvn]

Bonsoir à tous

@tournesol : merci

@catamat :
l'endomorphisme g est déjà injectif (puisque f l'est )
et H est de dimension finie, donc g est bijectif (le théorème classique) .
Donc il existe un vecteur x de H tel que g(x) = y , et par là f(x) = y
Comme y est fixé arbitrairement, f est surjectif.

Il ne me semble pas qu'on puisse aboutir si on prend seulement Vect(a,b)
qui ne contient pas tous les vecteurs de E...
Cette réponse vous convient elle ?
Cordialement

[tournesol]

On peut aboutir cependant avec vect(y,b)
Cela permet aussi de chercher l'antécédent de y sous la forme y+ub
On obtient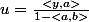 ce qui fait apparaitre la nécessité d'avoir

[Rdvn]

En effet la recherche de l'antécédent sous forme y+ub est intéressante, puisqu'on passe de
"il existe un antécédent" à "voici un antécédent" , ce qui est bien mieux.

Je dois bien admettre que je n'avais pas cherché plus loin après avoir trouvé une solution
(cette habitude d'en faire le moins possible !)

En revanche passer par Vect(y,b) ne me parait pas améliorer la solution que j'ai proposée,
je n'ai pas approfondi mais il me semble qu'on alourdit la rédaction

[tournesol]

On alourdit pas la rédac. On remplace H par vect(y,b) qui est stable par f.
L'interet de remarquer ce sous espace , c'est que l'on peut alors calculer l'antécédent de y sous la forme y+ub et surtout que la condition détermine son domaine de calculabilté.
Bien entendu , ces considérations grèvent la vitesse de résolution qui doit être optimale en concours , d'où l'interet de ta solution qui maintient l'optimalité de cette vitesse .

[catamat]

Ok merci à vous deux j'ai en effet très bien compris.

[Rdvn]

Bonjour à tous
@catamat : OK
@tournesol :
il est vrai que la démonstration ne s'alourdit pas.
En un premier temps, mettre a dans H me semblait très naturel, mais effectivement on peut s'en dispenser.
A titre de curiosité j'ai repris le problème de chercher explicitement l'antécédent de y dans H,
on y arrive, c'est juste un peu plus long.