Limites en 0+

par **forza** » 29 Déc 2006, 11:46

bonjour

voila,Je n'arrive pas a montrer que xln(x)-x tend vers 0 en 0+

en fait j'arrive pas a me séparer des formes indéterminées

Merci d'avance

bonne fetes de fin d'année

par **anima** » 29 Déc 2006, 11:55

forza a écrit:bonjour

voila,Je n'arrive pas a montrer que xln(x)-x tend vers 0 en 0+

en fait j'arrive pas a me séparer des formes indéterminées

Merci d'avance

bonne fetes de fin d'année

Je ne sais pas si ma manip' est dans l'art des maths, mais j'ai levé la forme indéterminée. En effet, quand x->0 en étant positif, e/x tend vers e, donc le ln tend vers 1, donc le tout tend vers 0

par **fonfon** » 29 Déc 2006, 12:01

salut,

tu n'as pas vu en cours que :

par **forza** » 29 Déc 2006, 12:08

chez moi e/x si x-> 0 ca fait + inf non ?

par **anima** » 29 Déc 2006, 12:29

forza a écrit:chez moi e/x si x-> 0 ca fait + inf non ?

Pardon...Mon erreur. Toujours indéterminée alors :hum:
Le pire, c'est que je savais la prouver il y a 1 mois...

par **fonfon** » 29 Déc 2006, 12:42

ben, sinon tu fais un cgangement de variable

tu poses X=1/x donc comme x->0+ alors 1/x>+inf donc X->+inf

on obtient:

de là tu s quand même dû voir que

et que

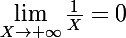
donc

A+

par **fonfon** » 29 Déc 2006, 12:47

ben, sinon tu fais un cgangement de variable

tu poses x=1/X donc comme x->0+ alors 1/x>+inf donc X->+inf

on obtient:

de là tu as quand même dû voir que

et que

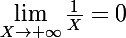
donc

A+

Limites en 0+

limites en 0+

Qui est en ligne