Fonctions

[lety59]

Bonjour, voilà j'ai un exo a faire pour la rentrée mais je n'ai pas trop compris, si quelqu'un pourrait me venir en aide ce serait gentil.
Voici l'énoncé:

f est la fonction définie sur R* par:

f(x)=1/x+4x²

1) déterminer le sens de variation de f sur ]-inf; 0[
2)a) construire, dans un même repère, les représentations graphiques des fonctions x->1/x, x->4x² et de la fonction f sur l'intervalle ]0;2].
b) Conjecturer à partir de la courbe représentant f le sens de variation de f sur ]0;2]
c) avec la calculatrice tracer la courbe représentant f sur ]0;1000]
conjecturer le sens de variation de f sur ]0;+inf[


voilà merci a ceux qui pourront m'aider! bonne soirée

[kidibou]

pour le 1), utilise la dérivée
si tu le n a pas encore fais, utilise la caractérisation des fonctions croissantes et decroissantes.

tu prend x

[lety59]

UP s'il vous plait

[Purrace]

Calcul la derivee de ta fonction et etudie son signe qui va te donne acces aux variations de la fonction f.

[lety59]

Calcul la derivee de ta fonction et etudie son signe qui va te donne acces aux variations de la fonction f.

comment faire pour calculer sa dérivée ?

[math*]

C'est du cours ça ! :triste:

[lety59]

C'est du cours ça ! :triste:

mais j'ai jamais vu ça moi :doh:

[math*]

Tu n'as pas encore étudier les dérivées ?
Tu aurais du le dire !!
(non je sais, si tu ne les as pas étudiées, tu ne pouvais pas savoir qu'il fallait dire que tu ne les avais pas étudiées, puisque ne sachant pas ce que c'est, tu ne pouvais pas non plus savoir qu'elles te seraient utiles....... :dodo: )

Oui donc là, c'est un tout autre problème.
Sur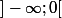 1/x et 4x² sont décroissantes donc la somme est...

[lety59]

Moi j'ai fait de la maniére suivante mais je sais pas si c'est bon:

1) Le sens de variation de 1/x sur ]-inf;0[ est décroissant car une fonction inverse est toujours décroissante

Le sens de variation de 4x² sur ]-inf;0[ est décroissant car la fonction carrée est tjrs décroissante sur ]-inf;0[

donc la fonction f(x)=1/x+4x² sera décroissante car on sait que u+v est décroissante si u et v sont décroissants

[maturin]

très bien c'est ce qu'il fallait faire.

Et si tu veux montrer que 1/x et x² sont bien décroissantes il faut prendre la définition :
pour tout x,y de ]-inf,0[ tel que xf(y)

enfin tu as aussi le droit de l'afirmer comme tu l'as fait car 1/x et x² sont des fonctions classiques dont tu dois connaitre le sens de variation
(en fait cela dépend si ton niveau te permet de dire que 1/x et x² sont des fonctions classiques :hum: )

[lety59]

Ouais, je ressort ça de mon cours sur les fonctions de référence ;)

[lety59]

Pouvez vous me dire si ceci est bon??

[maturin]

mes commentaire sur el graphique:

pour la fonction 4x² elle ressemble à peu près à ce que tu as tracé, juste vérifie sur ton graphe mais la fonction x² est "arrondie" en x=0 et est tangeante à l'axe des abscisses. J'ai l'impression sur la photo que tu l'a fait un peu en pointe.

sinon pour 1/x ca a l'air correct

et pour la courbe verte je sais pas ce que c'est

si c'est sensé être la courbe 4x²+1/x c'est pas ça et en plus tu l'as déssinée que sur ]0,+inf[

grosso modo pour tracer la courbe 4x²+1/x tu fais la somme de tes 2 courbes.
donc sur ]-inf,-1[ ta courbe être proche et un peu en dessous de 4x² (car 1/x petit). Sur ]-1,1[ elle va etre proche de 1/x et un peu au dessus (car 4x² sera petit et 1/x grand). Sur ]1,+inf[ ta courbe va etre proche de 4x² et un peu au dessus car 1/x petit.

La difficulté c'est aux alentours de -1 et 1 où la le mieux c'est de calculer qq valeurs de points.

[lety59]

Oui c'est parce que dans l'énoncer ils demandent de la tracer sur l'intervalle ]0;2], merci pour toon aide je vais vérifier ça, par contre peux tu m'aider pour le reste de l'exo ?

c'était:

b) Conjecturer à partir de la courbe représentant f le sens de variation de f sur ]0;2]
c) avec la calculatrice tracer la courbe représentant f sur ]0;1000]
conjecturer le sens de variation de f sur ]0;+inf[


Parce qu'en fait je ne sais pas ce qu'est que "conjecturer"

merci d'avance et bonne soirée

[maturin]

"conjecturer" ça veut dire "trouver par intuition" ou un truc comme ça.
Concerneant ton problème ça veut dire qu'il faut que tu te serve de la courbe pour trouver le résultat.

Pour tracer ta courbe tu calcules la valeur en x=0.25, x=0.5, x=0.75....x=2 sachant qu'en x=0 elle a une asymptote verticale comme la fonction 1/x.

Donc là tu dois voir que sur ]0;2[ ta courbe part de +inf en 0+, qu'elle décroit jusqu'à un certain point puis recroit jusqu'en x=2.


Le minimum de cette courbe est en x=0.5 où f(x)=4. Pour savoir le retrouver il faut savoir calculer une dérivée et faire une étude de fonction. Si tu ne connais pas ça c'est pas grave tous les points que tu auras tracés te permettrons de tracer la courbe correctement.

[lety59]

Merci pour ton aide, penses tu que, cette fois ci, ma courbe est bonne?


Et pourrais tu m'aider une nouvelle fois concernant la dernière question qui est:

avec la calculatrice tracer la courbe représentant f sur ]0;1000]
conjecturer le sens de variation de f sur ]0;+inf[


je ne sais pas tracer une courbe a la calculatrice :s

merci beaucoup

bonne soirée

[maturin]

ta courbe verte a déjà une meilleure tête.
Tu peux encore un petit peu améliorer:
- en dessinant l'asymptote verticale en 0+ (si tu calcules le point d'abscisse x=0.01 tu verras que ça monte très haut)
- en arrondissant un peu la courbe en x=0.5, là tu l'as dessiné pointue alors qu'une courbe classique n'est jamais pointue


sinon sur ]0,1000] ça fera pareil que ce que tu as fait là.
Plus x est grand plus d3 sera proche de d2
Plus x se rapproche de 0 plus d3 est proche de d1.
et c'est déjà le cas sur ton dessin donc y aura pas grand chose à voir de plus après.

Pour le sens de variation tu conjoncture donc
f décroissante sur ]0,0.5] f croissante sur [0.5,+inf[

pour ta calculette je ne peux t'aider il faut voir le mode d'emploi, en général t'as un menu graph où tu entres l'équation y=f(x) et un autre menu où tu entre les axes.

[lety59]

Merci pour ton aide mais je ne sais pas ce qu'est "l'asymptote", je n'ai pas du le voir en cours :s

encore merci

[maturin]

une asymptote c'est une branche qui part vers l'infini verticalement.
Comme la fonction 1/x qui a une asymptote en x=0.

On peut aussi parler d'asymptote horizontale (dans ce cas c'est que quand x tend vers +inf alors ta courbe reste sur la même valeur, y=0 est une asymptote à la fonction y=1/x)