Raisonner, ce n'est que du plaisir...

[berbera]

bonjour,
j'ai ce dm à faire pendant les vacances et je bloque complètement parce que la fonction est complexe.je sais montrer qu'une fonction est continue, dérivable, trouver les asymptotes, la convergence, la limite mais avec cette fonction particulière, je n'arrive pas à m'en sortir, je ne sais pas comment procéder. pourriez vous me donner quelques pistes ?

On considère la fonction de la variable réelle définie par

Si x<-1 f(x)= - racine de (x²+2x+2)
Si x compris entre -1 et 1 f(x)= sin ( P / 2 x)
Si 1 < x f(x)= racine de (x²-2x+2)

1. montrer que f est continue et dérivable sur R.
2. donner le tableau de variation de f et donner ses asymptotes en +infini et - infini.
3. soit (Un) définie par :
Uo>0
Un+1= f(Un) pour n supérieur ou égal à 0
Montrer que Un converge et donner sa limite.

je vous remercie d'avance.

[nabodechimie]

raisonner, ce n'est que du plaisir
tout à fait

[Zebulon]

Bonsoir,

On considère la fonction de la variable réelle définie par

Si x<-1 f(x)= - racine de (x²+2x+2)
Si x compris entre -1 et 1 f(x)= sin ( P / 2 x)
Si 1 < x f(x)= racine de (x²-2x+2)

1. montrer que f est continue et dérivable sur R.

je suppose que pour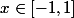 , c'est .
Pour montrer que f est continue, il faut montrer que f est continue sur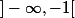 , que f est continue sur ]-1,1[, sur [ (jusque-là, ce sont des théorèmes)
et que f est continue en -1 et en 1 : il faut montrer que

et .