Cadeau du père Nöel

par **darkmaster** » 24 Déc 2006, 23:52

Voici un petit cadeau du père Nöel:
Soit une fonction

tel que

pour tous

.
On définit

avec

.
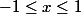
Déterminer les valeurs max et min de

sur

Joyeux Nöel!

par **MikO** » 25 Déc 2006, 11:26

voila qui devrait simplifier

par **khaclong** » 27 Déc 2006, 01:41

darkmaster a écrit:Voici un petit cadeau du père Nöel:
Soit une fonction tel que pour tous .
On définit avec .
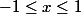
Déterminer les valeurs max et min de sur
Joyeux Nöel!

j'ai trouvé une solution pour ce problème

Alors,on a

,

et on prend y=1-x,on aura

Donc,

on utilise x+y=1 et xy=u;on aura

on a

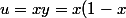Avec

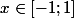
,on aura

on étudie g(x)=h(u) avec

on trouvera max et min de h(u)

par **darkmaster** » 27 Déc 2006, 02:02

Je suis ok, je crois que c'est la méthode la plus courte du problème. La clé est exprimer l'expression en fonction de (xy).
Enfin le papa Nöel est heureux :we:

Cadeau du père Nöel

Cadeau du père Nöel

Qui est en ligne