Réduction des endomorphismes : f de Rn[X]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
emkb
- Messages: 1
- Enregistré le: 21 Mai 2022, 19:24
-
par emkb » 21 Mai 2022, 19:52
Bonsoir,
Je suis bloquée sur un exo avec un endomorphisme de c.
Enoncé :Soient
,
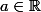
et
l'endomorphisme de
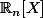
défini par :
,
 = (X - a).P' + P - P(a))
.
1. Déterminer
)
et
)
.
2. Déterminer les valeurs propres de
.
Pour le moment j'ai posé :
,
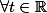
 = \sum_{i=0}^na_it^i)
Et :
 \Leftrightarrow ... \Leftrightarrow \sum_{i=0}^nx_i(i(t^i-at^{i-1}) + (t^i - a^i)) = 0)
Mais je peux pas dire que les termes de la suite sont tous positifs ou négatifs donc je peux pas avancer dans mon calcul, et je ne sais pas comment faire autrement (je voulais après utiliser le théorème du rang pour avoir
).
Est-ce que quelqu'un peut m'aider svp ?
Merci d'avance !
emkb
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
par Kolis » 23 Mai 2022, 07:29
Correction :
)
et non
)
.
Pour le noyau cherche, en fonction du degré de
qui n'est pas obligatoirement
, le degré de
P'+P)
.
Pour les valeurs propres, écris la relation voulue et travaille avec des fonctions réelles d'une variable réelle. Attention, les solutions de l'équation différentielle doivent être polynomiales...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
