Une inégalité

[khaclong]

Soit

et

Montrez que

[darkmaster]

Salut, mon ami
Je suis surpris que tu retiens encore ce problème, ça fait trop longtemps depuis le temps que l'on a apprendu celui-là.
Je vais essayer de démontrer encore une fois cette inégalité le matin. Maintenant je dois dormir. :dodo:

[darkmaster]

Salut, mon ami
Je suis surpris que tu retiens encore ce problème, ça fait trop longtemps depuis le temps que l'on a apprendu celui-là.
Je vais essayer de démontrer encore une fois cette inégalité le matin. Maintenant je dois dormir. :dodo:

Je change ma décision. Je viens de souvenir la solution. :zen: Alors, on ne doit pas attendre le matin. :id:

On va montrer que
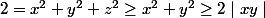
on a donc
Par Cauchy-Schwartz:

Alors qui conduit le résultat.