Nombre complexe et trigonométrie

[salyguya]

ok bon je vais essayer de faire la fin demain et si vraiment je vous redis si j'y arrive sinon j'espère que ma professeur puisse m'aider à la rentrée pour les dernières petites questions

[salyguya]

après je ne vois pas très bien comment tout ceci pourrait donner du cos(...)/sin(...) après j'ai pas encore fait les calculs donc je pense juste que c'est un peu obscur pour moi encore.

[catamat]

A quoi est égal

où q est un réel ou complexe différent de 1 ?

[salyguya]

Bonjour
3°)a)
Forme trigonométrique de z :
Forme algébrique de z :

On en tire par identification et

On peut donc remplacer x et y dans l'équation de la droite pour obtenir la relation demandée.

j'ai compris le raisonnement mais une fois psin(teta) = -pcos(teta) + 2 je ne vois pas comment on peut obtenir p=sqrt(2)/cos(teta-(pi/4) en faite c'est surtout le cos (teta-pi/4) je ne comprends pas parce que je réussi à trouver p=2/(sin(teta)+cos(teta)

[salyguya]

A quoi est égal

où q est un réel ou complexe différent de 1 ?

c'est un multiple de q, je pense pas que se soit la réponse attendue...désolé

[Pisigma]

Bonjour
3°)a)

j'ai compris le raisonnement mais une fois psin(teta) = -pcos(teta) + 2 je ne vois pas comment on peut obtenir p=sqrt(2)/cos(teta-(pi/4) en faite c'est surtout le cos (teta-pi/4) je ne comprends pas parce que je réussi à trouver p=2/(sin(teta)+cos(teta)

en multipliant les 2 membres de (*2) par et en tenant compte de (*1) on peut obtenir

[salyguya]

ok, juste pour savoir mais (*2) n'est pas une multiplication, ensuite je suis vraiment désolé mais je ne comprends pas comment vous êtes passé de la ligne avec le p en facteur commun au résultat. Merci vraiment en tout cas de m'aider autant je me sens un peu nul là...

[Pisigma]

(*2) signifie l'équation n0 2

en multipliant les 2 membres de (*2) par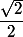

écris un peu la ligne obtenue après multiplication

[catamat]

A quoi est égal

où q est un réel ou complexe différent de 1 ?

c'est un multiple de q, je pense pas que se soit la réponse attendue...désolé

Ceci concernait le 2eme exercice

Somme des termes d'une suite géométrique de raison q...

[salyguya]

A quoi est égal

où q est un réel ou complexe différent de 1 ?

c'est un multiple de q, je pense pas que se soit la réponse attendue...désolé

Ceci concernait le 2eme exercice

Somme des termes d'une suite géométrique de raison q...

Ah oui OK le 2e exercices aussi c'est une suite géométrique ?

[catamat]

Oui
avec q=

[salyguya]

Oui
avec q=

OK... Et normalement j'utilise la formule de la somme d'une suite géométrique et on trouve ce qu'on devrait trouver, ok merci j'essaye cette après midi dès que je suis chez moi !

[Pisigma]

finalement as-tu finalisé l'autre exercice?

[salyguya]

finalement as-tu finalisé l'autre exercice?

alors si vous parlez de l'exercice avec teta oui j'ai finalement réussi j'ai juste pas compris direct l'autre exos avec la suite géométrique j'ai juste la somme à montrer sinon j'ai réussi les autres questions.

[salyguya]

(*2) signifie l'équation n0 2

en multipliant les 2 membres de (*2) par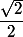

écris un peu la ligne obtenue après multiplication

si j'ai bien compris le sqrt2/2 c'est cos(pi/4) et sin(pi/4) donc ca se simplifie en cos de teta-pi/4
donc j'ai finalement que p = sqrt(2)/[(sqrt(2)/2)sinteta+costeta]

[salyguya]

j'ai oublié une ou deux parenthèses...

[salyguya]

Oui
avec q=

OK... Et normalement j'utilise la formule de la somme d'une suite géométrique et on trouve ce qu'on devrait trouver, ok merci j'essaye cette après midi dès que je suis chez moi !

En faite non je sais pas pourquoi j'ai dis ça

[salyguya]

j'essaye donc de mettre tous les thermes à la forme exponentielle, pour ensuite montrer que c'est une suite géométrique de raison q, cependant sin(x)=ie*ix dois je garder le i devant ?

[salyguya]

j'ai donc supposer qu'il fallait garder le i devant j'ai don finalement utiliser la formule d'une somme d'une suite géométrique mais j'ai un problème et je suis coincé j'ai vu votre factorisation avec des exponentielle - 1 mais je n'y arrive quand même pas je suis au début de la formule j'ai uniquement changé ceux par quoi il fallait que je change.

[Pisigma]