Ouvert connexe privé d'un élément

[BoredKangaroo]

Bonjour, je suis face à un exercice que je ne parviens pas à résoudre.

Montrer que si U est un ouvert connexe non vide de R^2 (muni de la norme associée à la distance euclidienne) alors, pour tout x de U, U \ {x} est connexe.

J'ai tenté d'utiliser les différentes caractérisations des espaces connexes que je connais mais je ne parviens jamais à conclure.
Par exemple, si je considère V un ouvert-fermé de U \ {x}, je ne parviens pas à montrer que l'union de V et de {x} est un ouvert de U, ce qui me permettrait ensuite de conclure. Si je considère une fonction de U \ {x} dans {0, 1}, je ne parviens pas non plus à en dire quoi que ce soit qui pourrait m'aider.

Auriez-vous une idée pour me débloquer ?

[GaBuZoMeu]

Bonjour,

Puisque est ouvert, il contient un disque ouvert de centre .
Un disque ouvert privé de son centre est-il connexe ?
On peut utiliser le fait qu'un ouvert connexe de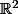 est connexe par arcs.

[BoredKangaroo]

Merci beaucoup, j'ai réussi l'exercice grâce à toi !

[GaBuZoMeu]

Avec plaisir.