Nombre complexe et trigonométrie

[salyguya]

Bonjour, voici 1 heure que je suis bloqué sur mon devoir maison en maths experte. J'ai compris certaines questions mais la plupart sont très obscure à mes yeux rien que la 1er question j'ai du mal même avec l'aide surtout quand j'essaye de passer (si ma méthode est juste) l'inéquation avec le cosinus.
voici l'exercice qui me pose problème (je n'ai pas regardé l'autre encore...)
Le plan es rapporté à un repère orthonormé direct (0;OU;OV)
on note D la droite d'équation y=-x+2
a) θdésigne un nombre réel
montrer que si θ appartient à ]-(π/4) ; 3π/4[, alors θ - π/4 > 0
b) Exprimer cos(θ - π/4) en fonction de cos(θ) et sin(θ). (j'ai un peu près compris celle ci on utilise la formule de soustraction et on remplace les valeurs qu'on sait grâce au cercle trigo)
3. M désigne un point du plan complexe d'affixe non nulle z
on note p=|z| le module de z et θ = arg(z) un argument de z.
les nombres p et θ sont appelés les coordonnées polaires du point M
a) montrer que si le point M appartient à la droite D, alors les coordonnées polaires vérifient
(*)p = sqrt(2)/ cos(θ - π/4) avec θ appartient à ]-(π/4) ; 3π/4[
b) réciproquement, montrer que si les coordonnées polaires de M vérifient la relation (*) alors le point M appartient à la droite D.
4. tracer la droite D dans le repère orthonormé direct
Placer l point M pour chacune des valeurs
θ = 0
θ = π/4
θ = π/2
dans chaque cas calculer p.
Voici l'exercice, j'espère que vous arriverez à m'aider, j'ai essayé et comme dit je n'ai pas réussi beaucoup de chose... Merci d'avance pour l'aide ! Pendant ce temps j'essaye l'autre exo !

[Pisigma]

Bonjour,

je n'ai pas réussi beaucoup de choses...

montre nous ce que tu as fait, où tu bloques

sais-tu ce que sont les coordonnées polaires?

[Rdvn]

Bonjour
Je pense qu'il y a une erreur au a) :
( notant t pour thêta) il faut montrer cos(t-Pi/4) > 0
Il me semble qu'il n'y a rien au programme de terminale sur les coordonnées polaires en
général, et qu'il faut s'en tenir à ce qui est dit en texte au 3 .
Je n'ai vraiment pas la disponibilité pour suivre davantage et je passe mon tour
Bon courage à tous

[salyguya]

Alors non je 'e sais pas ce que c' est les coordonnées polaires et j'aurais du me documenter mais j'ai oublié pour la 2a il y a une aide qui est : placer teta sur un cercle trigo puis teta-pi/4 pour visualiser (j'ai pas compris) et piur justifier commencer par la démonstration :-pi/4<teta < 3pi/4 et pour le programme de terminale c'est en option maths experte après oui ce dm est pour ceux qui souhaite continuer les maths l'année pro elle l'a donc fait assez difficile. Grâce à l'aide j'ai donc soustrait par-pi/4 partout avec le début de la démonstration puis je voulais le mette au cosinus mais conisus et négatif puis positif périodiquement et ça me donne finalement que cos(teta-pi/4) et plus petit et plus grand que 0 oulah j'ai mal expliquer je crois

[salyguya]

si vraiment mon DM repose sur la partie A de l'exo 111 page 91 et l'exo 109 p89 celui ci j'ai juste pas reussi la a

[salyguya]

Du manuel hyperbole option maths experte excusez moi pour les fautes de frappe et d'orthographe

[catamat]

Bonjour
3°)a)
Forme trigonométrique de z :
Forme algébrique de z :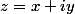

On en tire par identification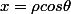 et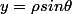

On peut donc remplacer x et y dans l'équation de la droite pour obtenir la relation demandée.

[salyguya]

Merci beaucoup pour la 3a et réciproquement je prends donc le "problème à l'envers"

[Pisigma]

a) il suffit de résoudre

je suppose que tu as déjà résolu des inéquations trigonométriques

[salyguya]

je peux regarder mais je n'ai jamais résolu (enfin je crois) d'inéquations trigonométriques mais je pense que les explications sont dispo, mais je dois donc trouver la solution ou l'ensemble des solutions pour lequel ils sont supérieur à 0

[salyguya]

et pour la 2b ja méthode que j'ai un peu près expliquer semble-t-elle juste ?

[Pisigma]

il faut appliquer la formule cos(a-b)=...; qu'as-tu trouvé?

[salyguya]

Oui je l'ai dans mon cours, et ensuite remplacé son et cos de-pi/4 par les valeurs dans le cercle trigo

[Pisigma]

donc tu as pu répondre à la question?

[Pisigma]

je peux regarder mais je n'ai jamais résolu (enfin je crois) d'inéquations trigonométriques mais je pense que les explications sont dispo, mais je dois donc trouver la solution ou l'ensemble des solutions pour lequel ils sont supérieur à 0

donc c'est OK?

[salyguya]

je peux regarder mais je n'ai jamais résolu (enfin je crois) d'inéquations trigonométriques mais je pense que les explications sont dispo, mais je dois donc trouver la solution ou l'ensemble des solutions pour lequel ils sont supérieur à 0

donc c'est OK?[/quoteperso c'edt bon il reste donc juste la 2a que je ne comprends vraiment pas et la 4 j'ai un peu près cerné ceux qu'il faut faire et pour l'autre exo j'ai pas réussi la 1er question mais celui là je peux me débrouiller normalement

[salyguya]

excusez moi mais j'ai fais le 2e exercice et j'ai pas réussi une question :
pout tout entier naturel supérieur ou égal à 2
Sn =sin(pi/n)+sin(2pi/n)+...+sin((n-1pi/n))
démonter que Sn=cos(pi/2n)/sin(pi/2n)

[Pisigma]

il y a une coquille dans l'énoncé, c'est



passe par la forme exponentielle des nombres complexes en tenant compte que

[salyguya]

C'edt un r devant la forme expodentielle ? Si oui le t signifie le module on est d'accord ? Je vais essayer de le faire, on a à peine commencer le chapitre en tout cas merci !

[catamat]

Devant 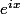ce symbole désigne la partie imaginaire (c'est la lettre I majuscule)

Une astuce de factorisation, bonne à connaitre :