Bonjour,
Merci pour vos réponses et désolé pour le temps de latence. Mais avec les fêtes...
effectivement, j'aurai du faire attention en recopiant, il n'y a pas d'alpha sous la racine carrée et c'est un B à la place du alpha sous l'exponentielle.
Pour l'intégration par partie, je crois que si
\frac{1}{x}sin(\alpha x)])
est nulle c'est parce que c'est une fonction impaire intégrée sur

si je répète ensuite la procédure d'intégration par partie
avec
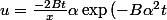)
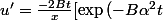-(B\alpha^2 t)\exp{(-B\alpha^2 t)])
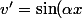, v= -\frac{1}{x}\cos(\alpha x))
j'obtiens :
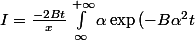}\sin{(\alpha x)}}d\alpha = <br />\frac{-2Bt}{x^2}[-\alpha exp(-B\alpha^2 t)\cos(\alpha x)] + <br />\frac{-2Bt}{x^2}\int_{\infty}^{+\infty}<br />[(-Bt\alpha^2)\exp{(-B\alpha^2 t)}+\exp{(-B\alpha^2 t)}]\cos{(\alpha x)}}d\alpha)
Bref je tourne en rond...
Et pour l'autre méthode, ça fait malheureusement longtemps que je n'ai pas touché à la théorie des fonctions holomorphes et j'ai bien peur que tes explications ne soient un peu succinte pour mes bribes de souvenirs...
Si tu pouvais développer un peu plus
Merci