Existence d'un équilibre de Nash dans un jeu concave

[Magnus]

Pour montrer l'existence d'un équilibre de Nash, je suis resté bloqué sur un résultat qui m'indique que est semi-continue supperieurement avec :



Notons ici que :



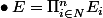
avec est convexe, compact

est concave sur pour tout fixé dans

est continue sur


Donc ma question est la suivante:

Comment demontrer que est semi continue supperieurement?

[Doraki]

Tu peux rappeler ce que veux dire une fonction semicontinue supérieurement lorsque la fonction n'est pas à valeurs dans R ?

Gamma est à image dans l'ensemble des parties non vides fermées (et même convexes) de E.
On peut mettre une distance dessus et un ordre partiel.
On peut même mettre une sorte de "semidistance" s(X,Y) = sup pour x dans X de d(x,Y)

Peut-être qu'il faut montrer que pour tout x de E et epsilon > 0 il existe delta>0 tel que |x-y| <= delta => s(x,y) <= epsilon ?