Bonjour,
je suis bloqué sur cet exercice :
Soit (E, +, .) un espace vectoriel de dimension finie n>=1
u, v appartiennent à l'ensemble des A.L de E dans E.
On suppose que dim(im(u+v)) = dim(im(u)) + dim(im(v))
Montrer que : - E = ker(u) + im(v) = ker(v) + im(u)
- im(u) inter im(v) = {0}
le prof m'a donné comme indice le fait que pour montrer que E = A + B on peut partir du fait que dim(E) = dim(A+B) = dim(A) + dim(B) - dim(A inter B) mais je n'avance pas...
Merci pour votre aide
Exercice de dimension, noyau, image (niveau maths L1)
4 messages
- Page 1 sur 1
Re: Exercice de dimension, noyau, image (niveau maths L1)
Bonsoir,
Tu peux remarquer pour commencer que l'image de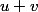 est toujours contenue dans la somme des images de
est toujours contenue dans la somme des images de  et de
et de  .
.
Tu peux remarquer pour commencer que l'image de
Re: Exercice de dimension, noyau, image (niveau maths L1)
Il faut d'ailleurs corriger la première question, sans doute en 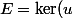+\ker(v)) .
.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
