Rayon de convergence de série entière solution d'ED

[daricbeyer]

L'équation différentielle est .
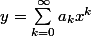
Sachant que la solution est de la forme , j'ai une relation de récurrence pour les coefficients : .
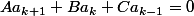
De plus, pour très grand, on voit que , donc .
A partir de là, je dois calculer le rayon de convergence de la solution , mais je ne vois pas comment je dois faire. J'ai essayé avec le critère du quotient mais ça ne donne rien de bien.
Il y a un théorème sur les ED du 2ème ordre , où sont analytiques, qui dit que le rayon de convergence de la solution est plus grand que le plus petit rayon de convergence des séries définies par et . Mais je vois pas comment appliquer cela ici, sachant qu'on a une ED du premier ordre.