Intégrale trigonométrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 08 Mar 2022, 09:56
par lefouineur » 08 Mar 2022, 09:56
Bonjour à tous,
Je cherche à démontrer que:
}dx=tg\frac{x}{2})
,
J'ai essayé de transformer l'écriture de sin(x) avec
=\frac{2t}{1+t^2})
mais ce n'est pas concluant.
Merci d'avance pour vos réponses Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Mar 2022, 10:32
par Pisigma » 08 Mar 2022, 10:32
Bonjour,
c'est normal que tu n'y arrives pas car c'est faux!
tu aurais du trouver
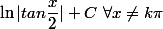
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 08 Mar 2022, 11:00
par lefouineur » 08 Mar 2022, 11:00
Bonjour Pisigma et merci pour ta réponse rapide,
En effet je me suis trompé, J'aurai du prendre mon formulaire. elle était dedans.
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Mar 2022, 11:04
par Pisigma » 08 Mar 2022, 11:04
il suffisait de poser tan(x/2)=t
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 08 Mar 2022, 12:05
par tournesol » 08 Mar 2022, 12:05
On peut aussi montrer que les deux fonctions ont la même dérivée.
-
catamat
- Habitué(e)
- Messages: 1364
- Enregistré le: 07 Mar 2021, 10:40
-
 par catamat » 08 Mar 2022, 12:19
par catamat » 08 Mar 2022, 12:19
Bonjour
On peut aussi poser x=2t donc dx=2dt et t =x/2
}dt=\int \frac{1}{sin t cos t}dt=\int \frac{1}{\frac{sin t}{cos t} cos^2 t}dt=\int \frac{tan' t}{tan t}dt=ln|tan t|=ln|tan(\frac{x}{2})|)
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 08 Mar 2022, 13:48
par tournesol » 08 Mar 2022, 13:48
Joli catamat!
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 08 Mar 2022, 14:22
par Pisigma » 08 Mar 2022, 14:22
une autre plus classique
}dx= \int \dfrac{sin (x)}{sin^2(x)}dx=\int \dfrac{sin (x)}{1-cos^2(x)}dx)
ensuite on pose
=t, -sin(x) dx= dt)
, il vient
}{1+cos(x)}=\dfrac{1}{2}\ln\dfrac{sin^2(\dfrac{x}{2})}{ cos^2(\dfrac{x}{2})}=\ln|tan(\dfrac{x}{2})|)
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 10 Mar 2022, 14:13
par lefouineur » 10 Mar 2022, 14:13
Merci à tous pour vos contributions
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 10 Mar 2022, 14:32
par Pisigma » 10 Mar 2022, 14:32
de rien

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités