Résolution équation du second degré

[Seldon²]

Bonjour,

Une question de mon dm me pose problème, je ne comprend pas la question ni comment je pourrai y répondre
Voici la question :

On dit que deux nombres positifs a et b respectent la « proportion d’or » (ou « proportion divine ») si
a/b=a+b/a
. Des des architectes tels Le Corbusier ou des artistes comme Dali utilisaient de tels nombres dans certains de leurs travaux.
1) On note x=a/b
cette proportion, que l’on suppose non nulle.
a/ En remarquant que a/b=a+b/a=1+b/a , montrer que x=a/b vérifie l’équation x(au carré)−x−1=0

J'ai deja essayé de remplacé x dans l'équation par 1-1/x car a/b= 1-b/a = 1- 1/a/b et que x = a/b mais cela n'a rien donné.

[Pisigma]

Bonjour,

[Seldon²]

ah oui pardon j ai mis un moins mais j avais bien mis un plus lorsque je l'ai résolu sur ma feuille.
Du coup est ce que c est la bonne piste ou il faut chercher ailleurs.

[GaBuZoMeu]

Bonjour,

Ne vois-tu pas comment passer de l'équation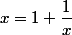 à une équation du second degré en ?

[Seldon²]

Bonjour,

est ce que cela marche : x = 1/x
x-1-1/x=0
je met tout au même dénominateur
(x^2-x-1)/x=0
x^2-x-1=0 * x
x^2-x-1=0

[Pisigma]

je ne comprends pas

est ce que cela marche : x = 1/x

d'où sors-tu ça?

[Seldon²]

Quand j ai recopié j ai oublié d ecrire le 1 devant le 1/x d'ou l'imcompréhension donc la première ligne corrigé est x=1+1/x

[Seldon²]

En fait je me demandais si je pouvais faire disparaitre le x à droite en le multipliant au 0

[Pisigma]

Houlà! si tu multiplies par 0 que devient le produit?

[GaBuZoMeu]

Bonjour,

Ce que tu as à faire, c'est de démontrer l'équivalence de

1) et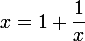

2) .

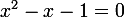Essaie de faire cette démonstration proprement : 1) entraîne 2), puis 2) entraîne 1).

[mathou13]

Bonjour,

On dit que deux nombres positifs a et b respectent la « proportion d’or » (ou « proportion divine ») si
a/b=a+b/a
. Des des architectes tels Le Corbusier ou des artistes comme Dali utilisaient de tels nombres dans certains de leurs travaux.
1) On note x=a/b
cette proportion, que l’on suppose non nulle.
a/ En remarquant que a/b=a+b/a=1+b/a , montrer que x=a/b
x=a/b=a+b/a=1+b/a
<->a/b-1-b/a=0
<->a^2b/ab^2-ab^2/ab^2-b^3/ab^2=0
<->ab/b^2-b^2/b^2-(b/a)*(b^2/b^2)=0
<->ab/b^2-b^2/b^2-(a/b-1)*(b^2/b^2)=0
<->ab/b^2-b^2/b^2-(ab/b^2-b^2/b^2)=0
<->(ab-b^2-ab+b^2)/b^2=0 or (ab+b^2=a^2 car a/b=a+b/a<->b(a+b/a)=a <-> ab+b^2=a^2).
<->(a^2-ab-b^2)/b^2=0
<->a^2/b^2-ab/b^2-b^2/b^2=0
<->(a/b)^2-a/b-1=0
or x=a/b
<->x(au carré)−x−1=0
vérifie l’équation x(au carré)−x−1=0