Voici une inégalité :
Montrer que
Une inégalité*
3 messages
- Page 1 sur 1
par musichien » 04 Aoû 2006, 10:47
On passe dans l'autre membre le dénominateur, et ça donne (somme symétrique (3,3,2))/2 inférieur à (somme symétrique (8;0;0))/2, ce qui est bien vrai (Muirhead).
par khaclong » 21 Déc 2006, 01:08
salut,je viens de trouver une autre solution pour ce problème
On peut utiliser l'inégalité suivant:
on aura:
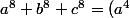^2+(b^4)^2+(c^4)^2\geq (ab)^4+(bc)^4+(ca)^4)
et
^4+(bc)^4+(ca)^4=(a^2b^2)^2+(b^2c^2)^2+(c^2a^2)^2\geq a^2b^4c^2+a^4b^2c^2+a^2b^2c^4=a^2b^2c^2(a^2+b^2+c^2)\geq a^2b^2c^2(ab+bc+ca))
on conduit que
}{a^3b^3c^3}=\frac1a+\frac1b+\frac1c)
on l'a montré
On peut utiliser l'inégalité suivant:
on aura:
et
on conduit que
on l'a montré
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :