Bonsoir,
Soit f une fonction continue de R dans R et pour tout x dans R, g(x)=intégrale( f(x+t)exp(t) )dt de 0 à 1.
Je dois montrer que g est de classe C1 et je dois exprimer g' en fonction de g et f.
Alors pour montrer que c'est C1, est ce que je dois utiliser que f(x+t)exp(t) est C1 par rapport aux deux variables ?
Donc g'(x)= intégrale( f'(x+t)exp(t) )dt mais après je n'arrive pas à continuer.
Merci beaucoup pour vos réponses
Fonction définie par une intégrale
3 messages
- Page 1 sur 1
Re: fonction définie par une intégrale
Bonjour,
Tu parles de la dérivée de alors que
alors que  est seulement supposée continue. Donc ça ne va pas.
est seulement supposée continue. Donc ça ne va pas.
Tu peux essayer le changement de variable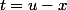 .
.
Tu parles de la dérivée de
Tu peux essayer le changement de variable
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
