Produit Scalaire Terminale

[GoldBear]

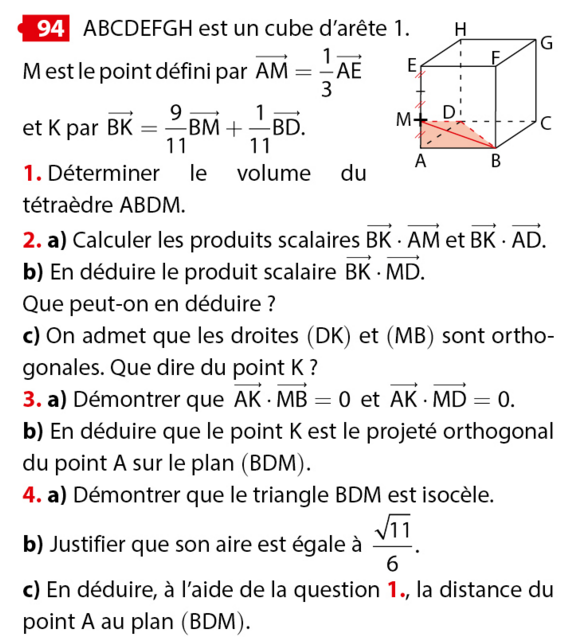
Bonjour. J'ai besoin d'aide pour faire cet exercice svp.
Merci

[mathelot]

Bonsoir,

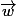
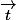
vocabulaire: un vecteur est combinaison linéaire des vecteurs , et s'il existe trois nombres réels a ,b,c (on les appelle des scalaires) tels que:




Données: On prend comme repère orthonormé de l'espace

Ainsi tous les vecteurs sont combinaison linéaire des trois vecteurs du repère. De plus, AB=AD=AE=1

[mathelot]

Question 1
Le volume du tétraèdre est donné par la formule:
où B est l'aire de la base et h la hauteur associée au sommet opposé


d'où

[GoldBear]

Merci pour cette première réponse. Néanmoins, pouvez-vous également m'aider pour les autres questions s'il vous plaît.
Merci d'avance

[mathelot]

oui, je peux t'aider. tu en es à quelle question ?

[mathelot]

Question 2.a
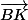
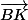
Ecris comme combinaison linéaire de (utilise la définition de) et décompose la formule de en utilisant la propriété de Chasles en passant par le point A.

[GoldBear]

Bonjour. Je n'avais réussi que la question 1 et je n'arrive pas à faire la suite.

[catamat]

Bonjour
Une autre façon pour , après développement il suffit de calculer et

Or =0 car les vecteurs sont orthogonaux (à justifier)

et car B se projette orthogonalement en A sur (AM)

Même chose pour le produit suivant.

[mathelot]

question 1 et je n'arrive pas à faire la suite.

Pour calculer un produit scalaire, il suffit d' exprimer les vecteurs du produit en fonction des vecteurs de base.
car ensuite on développe le produit et on utilise


et

[GoldBear]

Merci à tous pour vos réponses

[mathelot]

Question 2a.

j'explicite l'idée de catamat:

on veut calculer le produit


par linéarité, on a:




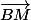
car se projette orthogonalement sur

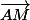
est nul car la droite (AM) est perpendiculaire au plan (BDA)



d'où


De même

[mathelot]

Question 2.b
Calcul de

on a:

[catamat]

Merci Mathelot.

[GoldBear]

Merci, grâce à vous j'ai pu trouver pour la 2-b)
BK.MD=BK.(AD-AM)
=BK.AD-BK.AM
=1/11 - 1/11
=0

On en déduit que les vecteurs BK et MD sont orthogonaux

[catamat]

Ok, donc qu'en déduit-on pour le point K dans le triangle DBM (question 2c) ?

Pour le 3)
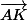
Pour le premier produit scalaire, remplacer par puis développer les deux produits scalaires obtenus sont nuls...

[GoldBear]

On en déduit que le point K appartient au triangle (BDM) ?

[catamat]

Certes mais c'est un point particulier de ce triangle

[GoldBear]

K est le centre du triangle (BDM) ?

[GoldBear]

De plus, avez-vous une astuce pour démontrer que AK.MD=0 ?

[catamat]

K est le centre du triangle (BDM) ?

Le centre de gravité ? non

Il y a trois points particuliers connus dès le collège qui sont les points de concours des médianes, des hauteurs et enfin des médiatrices, appelés respectivement centre de gravité, orthocentre et centre du cercle circonscrit.

Sinon pour le produit scalaire suivant, utilise la conclusion du 2b et intercale avec Chasles le point qui permet de l'utiliser.