Les limites de fonction (avec exponentielles)

[Oceane4002578809]

Bonjour à tous. J'ai un devoir de math à rendre pour la fin de semaine seulement voilà j'ai été confiné et je ne comprends pas vraiment ce que je dois faire...
Voici le sujet
Soit f la fonction défini sur ]0;+oo] par f(x)= (2e^x)+1/(e^x)-1 et Cf sa courbe représentative
1. Calculer la limite de f en 0+
2.a montrer que pour tout réel x de ]0;+oo], f(x)= 2+e^-x/ 1-e^-x
B. Calculer la limite de f en +oo
3. Justifier que la courbe Cf admet deux asymptotes que l'on précisera
4.a montrer que pour tout réel x de ]0;+oo], f'(x)= -3e^x/((e^x)-1)^2
B. construire le tableau de variation f sur ]0;+oo]

Voilà si quelqu'un pouvait m'aider se serait vraiment gentil. Je bloqué surtout sur les questions 2a et 4a

[azf]

Bonjour

J'essaye de décrypter f mieux vaut mettre des parenthèses superflue qu'en oublier

f(x)= (2e^x)+1/(e^x)-1

vous voulez dire ça



mais si c'est ça vos parenthèses sont mal faites

il fallait écrire f(x)= ((2e^x)+1)/((e^x)-1) voire f(x)= (2e^x+1)/(e^x-1)

mais mieux vaut en mettre plus que pas assez

(mais j'ai l'intuition que c'est ça)

[Oceane4002578809]

Oui désolé mais vous avez raison votre intuition est bonne !

[azf]

ok et pour la question 2a

f(x)= 2+e^-x/ 1-e^-x

vous voulez dire ça (je suppose sans être certain) ?

[Oceane4002578809]

Oui c'est ça, il fait vraiment que j'apprene à me servir des formules pour écrire comme vous...

[azf]

ok
et pour la question B
vous parlez de quel f?
là on a deux fonctions f
pouvez vous relire votre énoncé et voir si il est fidèlement recopié

[Oceane4002578809]

Je n'ai fait aucune faute c'est simplement que notre professeur nous laisse faire les deux et de choisir celle qui n'aura pas de forme indéterminée. Si je ne me trompes pas là première sera FI donc il faudra utiliser la deuxième pour tomber sur un nombre rond

[azf]

pardon mais vous écrivez B

où est A ?

est-ce que A et B sont deux exercices différents?

pouvez vous recopier l'énoncé

s'agit-il de

A soit ...
1)question
2)question

B) Soit ...
1)question
2)question

si c'est ça relisez votre premier post et on voit que c'est pas présenté comme ça

[Oceane4002578809]

Soit f la fonction défini sur ]0;+oo] par f(x)= (2e^x)+1/(e^x)-1 et Cf sa courbe représentative
1. Calculer la limite de f en 0+
2.A montrer que pour tout réel x de ]0;+oo], f(x)= 2+e^-x/ 1-e^-x
2B. Calculer la limite de f en +oo
3. Justifier que la courbe Cf admet deux asymptotes que l'on précisera
4A montrer que pour tout réel x de ]0;+oo], f'(x)= -3e^x/((e^x)-1)^2
4B. construire le tableau de variation f sur ]0;+oo]

Est ce plus compréhensible de cette façon ? Il ne s'agit que d'un seul et même exercice

[azf]

Pardon mais dans le même exercice je vois deux fonctions différentes du même nom f et on pose des questions sur f mais de laquelle des deux on parle?

Soit f la fonction défini sur ]0;+oo] par f(x)= (2e^x)+1/(e^x)-1
...
f(x)= 2+e^-x/ 1-e^-x

Je ne comprend pas l'énoncé
Je suis vraiment désolé j'espère que quelqu'un viendra

[azf]

ok je viens de comprendre l'énoncé pardon
c'est la même fonction

[azf]

pour la question 2a)

[azf]

...et pour la question 4a)

on profite du fait que f ne s'annule pas sur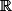

en appliquant la formule de dérivation

[catamat]

...et pour la question 4a)

on profite du fait que f ne s'annule pas sur

en appliquant la formule de dérivation

@Azf je suppose que tu voulais dire que v (f étant égal à u/v) ne s'annule pas sur Df ce qui permet de dire que f est dérivable sur Df.

Pour revenir sur la deuxième forme de la fonction f c'est une aide donnée à l'élève pour lui permettre de lever l'indétermination ici en +infini.

On aurait pu ne pas la donner et dans ce cas il aurait fallu, par exemple, mettre exp(x) en facteur dans les deux termes de la fraction.

[azf]

@Azf je suppose que tu voulais dire que v (f étant égal à u/v) ne s'annule pas sur Df ce qui permet de dire que f est dérivable sur Df.

Bonjour Catamat
oui