Bonjour,
On note
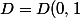)
le disque unité ouvert dans

,
)
les fonctions holomorphes
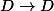
et
)
les fonctions polynomiales
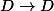
.
Je cherche à montrer que
)
est dense dans
)
pour la topologie de la convergence uniforme sur tout compact.
Pour cela, on sait que si
, \: f = \sum_{k=0}^{\infty}{\frac{f^{(k)}(0)}{k!}z^k})
. En d'autres termes, si l'on pose
}(0)}{k!}z^k})
,
_n)
converge vers

uniformément sur tout compact de

.
J'ai donc tenté de poser
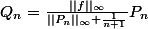
, où, étant donnée
)
,
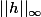
désigne "abusivement" la quantité
| \: : \: z \in D \, \})
(ce sup existe car
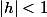
sur

).
J'essaie ensuite de montrer que
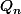
tend vers

uniformément sur tout compact :
Soit

un compact de

et soit
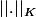
la norme "sup" sur

.
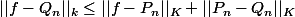
.
On sait que
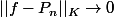
quand
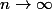
.
Mais pour le second terme, j'ai un peu plus de mal à justifier la convergence vers 0, que je vois pourtant intuitivement...
On a
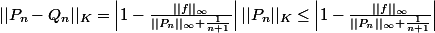
Ensuite, intuitivement, j'ai envie de dire que
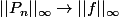
quand
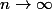
, mais je ne vois pas comment le justifier...
Voici ce que j'ai pour le moment :
Soit
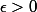
.
Par définition de la borne supérieure, il existe
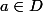
tel que
| \geq ||f||_{\infty} - \frac{\epsilon}{2})
.
Comme
 \longrightarrow f(a)})
, il existe
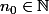
tel que, pour tout
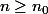
,
|-|f(a)|| \leq | P_n(a) - f(a) | \leq \frac{\epsilon}{2},)
ce qui implique
| \geq |f(a)| - \frac{\epsilon}{2} \geq ||f||_{\infty} - \epsilon)
Il faut ensuite montrer "l'autre sens", à savoir que pour

assez grand, on a aussi
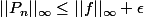
.
Et là, je suis bloqué...
Quelqu'un voit-il comment finir la preuve ?
