Inegalité de convexité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 18 Déc 2006, 14:04
par bibup » 18 Déc 2006, 14:04
Bonjour;
Je dois montrer que:
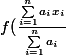)
=
}{\sum_{i=1}^n a_{i}})
avec
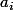
appartenant à R+*
Je sais que je dois le faire par récurrence, ça tombe sous le sens mais j'ai des soucis avec les sommes de i=1 jusqu'a n+1 au niveau du dénominateur.
Merci de m'indiquer le piege s'il y en a 1!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Déc 2006, 14:06
par fahr451 » 18 Déc 2006, 14:06
et si pour simplifier tu prenais tout simplement la somme des masses qui vaut 1?
ce qui revient à poser a'i = ai / somme des ai
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 18 Déc 2006, 14:08
par bibup » 18 Déc 2006, 14:08
je me suis trompé, il y a le signe

-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Déc 2006, 14:09
par fahr451 » 18 Déc 2006, 14:09
oui inférieur : l 'image du barycentre ( à masses positives)est inférieure au barycentre des images ce qui traduit que la courbe est sous les cordes.
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 19 Déc 2006, 17:13
par bibup » 19 Déc 2006, 17:13
comment peut-on déduire l'inégalité de Minkowski de cette inégalité?
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 19 Déc 2006, 17:15
par bibup » 19 Déc 2006, 17:15
est-ce que pour la récurrence, quand on pose le ai' il faut prendre au dénominateur une somme variant de j=1 à n au lieu de i?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 19 Déc 2006, 20:24
par fahr451 » 19 Déc 2006, 20:24
l'inégalité avec sigma des ai au dénominateur est exactement la même avec un sigma qui vaut 1 (poser ai' ..)
on fait une récurrence : on suppose la formule vraie au rang n
au rang n+1 on prend a(1) ,...,a(n+1) de somme 1
un des ai est non nul et différent de 1 sinon rien à faire; on peut supposer que c'est a(n+1)
on pose A = sigma (i = 1 ,..., n) de a(i) [ est non nul]
et y = sigma(i= 1,...,n) des a(i)xi / A
on a donc f (Ay+a(n+1)x(n+1) ) on applique l 'inégalité pour deux puis ensuite l hypothèse de récurrence au rang n .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités