Une équation implicite

[Kruslen]

Bonjour,

Je voudrais demander de l'aide aux utilisateurs de ce forum.

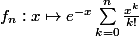
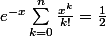
On peut montrer, à l'aide de la décroissance de la fonction sur R_{+} que l'équation admet une unique solution sur R_{+}. On peut aussi montrer que cette suite (x_{n}) est strictement croissante. J'aimerais maintenant savoir si elle converge. Avec une étude numérique, je pense que NON et que (x_{n}) tend vers l'infini, mais je n'arrive pas à l'établir...

Est-ce que quelqu'un voit comment faire ?

Bonne journée à tous,

Kruslen

[Ben314]

Salut,
Ta suite tend bien vers +oo et c'est evident :
Pour un M>0 fixé, la somme de k=1 à n des M^k/k! tend vers exp(M) donc fn(M) tend vers 1 ce qui, vu la décroissance de fn, prouve que xn>M à partir d'un certain rang.