Suites extraites

[Ssbb]

Bonjour, je voudrais savoir si (u2n) et (u3n) converge vers la même limite alors est ce que (un) converge vers cette même limite ?

Je pense que c’est faux mais je n’arrive pas à trouver de contre exemple.

Merci d’avance pour votre réponse.

[tournesol]

un=1 ssi n est premier , un=0 sinon .
Autrement dit :
remarque:
si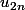 et 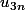convergent , alors elles ont la même limite puisqu'elles ont une suite extraite commune :
par contre peut avoir une autre limite .

[catamat]

Bonjour
Si on note {x} la partie fractionnaire de x soit x-E(x)
{}*{}

[tournesol]

Joli contre exemple catamat pour sa concision mais surtout pour son "endogénéité" ( n'utilise que les données de l'énoncé) .

[Ben314]

Salut,
Et si on suppose que la suite réelle est telle que, quelque soit le nombre premier , la suite extraite est convergente, il se passe quoi ?

[tournesol]

Ben314 .Je découvre ta question interréssante .
catamat , on a

[tournesol]

Toutes ces suites ont la même limite (immédiat) .
Pour la fonction caractéristique de l'ensemble des nombres premiers , tes suites extraites convergent vers 0 , mais toute les sous suite à indices premiers convergent vers 1 ...et pourraient même diverger si on prend au départ

[Ssbb]

un=1 ssi n est premier , un=0 sinon .
Autrement dit :
remarque:
si et convergent , alors elles ont la même limite puisqu'elles ont une suite extraite commune :
par contre peut avoir une autre limite .

Bonsoir, merci pour ta réponse tournesol, si j’ai bien compris u2n=u3n=0 car 2n et 3 n ne sont pas premiers donc elles convergent vers 0 mais la suite (un) n’a pas de limite car elle est alternée entre 0 et 1 ?

[Ssbb]

Bonjour
Si on note {x} la partie fractionnaire de x soit x-E(x)
{}*{}

Bonsoir Catamat et merci pour ta réponse, mais dans ton exemple, il n’est pas clair que (U2n) et (U3n) convergent

[tournesol]

La partie fractionnaire d'un réel est nulle ssi ce réel est un entier .
Donc u2n et u3n convergent vers zéro .
u(6n+1) converge vers 1/6
u(6n+5) converge vers 2/6

[azf]

Bonjour
Si on note {x} la partie fractionnaire de x soit x-E(x)
{}*{}

pardon si je dis une connerie et c'est possible aussi car mon histoire d'équivalence de suite est un peu hasardeuse car je ne dis pas comment réaliser cette équivalence en tout cas vu comme ça par moi sans entrer dans ma logique plus avant mais à part ça je trouve que E(x) est un peu ambigüe comme expression ou alors c'est la définition qu'on prend pour {x} qui n'est pas claire

sinon on peut faire
Ei(x) pour partie entière inférieure
Es(x) pour partie entière supérieure

pour
x=Ei(x)+{x}
pour
x=Es(x)+{x}

et pour tout rationnel positif x (et un réel peut s'encadrer entre deux rationnels) on peut alors trouver un naturel a et un naturel non nul b tel que alors

on sait alors qu'on aura toujours est un naturel

bon alors pour mon histoire on peut exprimer une équivalence de la suite initiale qu'avec des entiers pour peu qu'on se débarrasse du dénominateur b

[tournesol]

Par définition , la partie entière d'un réel x est le plus grand entier relatif inférieur ou égal à x .
Cette définition correspond à ta partie entière inférieure .
On la note E(x) ou encore [x] .
Caractérisation : k=[x] ssi ( ET )
La partie fractionnaire de x est , par définition , égale à x-[x] . On la note {x} .
En enlevant k aux trois membres de la double inégalité de caractérisation , on obtient

[Ssbb]

La partie fractionnaire d'un réel est nulle ssi ce réel est un entier .
Donc u2n et u3n convergent vers zéro .
u(6n+1) converge vers 1/6
u(6n+5) converge vers 2/6

Merci, effectivement c’est plus claire maintenant

[catamat]

Merci Tournesol pour avoir si bien expliqué mon exemple... Je n'avais pas vu la question qui m"était posée.

[azf]

Cette définition correspond à ta partie entière inférieure .
On la note E(x) ou encore [x] .

Merci pour la précision Tournesol
J'avais complètement oublié que j'avais dit quelque chose ici et en plus après ces quelque jours (édit j'ai posté ça en pleine nuit mais j'avais surtout sommeil) je ne comprends même plus ce que j'ai dit :
"équivalence de quoi ?" bref j'ai raconté n'importe quoi...