Exercice fonction constante TS

[Lmaths]

Bonjour,

Je bute sur une question de mon DM de maths :
"Soit f une fonction qui vérifie la condition 1 et soit g la fonction définie par : g(x) = f^2(x) - 2x pour tout x supérieur ou égal à 0. Démontrer que g est une fonction constante et déterminer cette constante. En déduire l'expression f(x) pour x réel positif."

Voilà la condition 1 : f(0) = 1 et f(x) * f'(x) = 1 pour tout x supérieur ou égal à 0.

Précédemment, nous avons montré que f'(0) = 1 et qu'une fonction vérifiant la condition 1 est nécessairement strictement positive (grâce à plusieurs questions : en montrant que f ne s'annulait pas sur [0;+∞[ , puis en montrant que s'il existe un réel a strictement positif tel que f(a)<0 alors f(x)=0 admet au moins une solution dans l'intervalle [0;a[ ).

Je ne vois pas comment avancer. Quelqu'un aurait-il une idée ?

[mathelot]

Bonsoir,
dérive la fonction g sur l'intervalle

si u est une fonction dérivable ,

[Pisigma]

Bonjour,

peut-être partir de la résolution de soit

[Lmaths]

Re-bonjour,

Alors du coup en dérivant j'arrive à :

g'(x) = f^2'(x) - 2
g'(x) = (1/f(x))^2 -2

Suis-je sur la bonne voie ?

[mathelot]

si u est une fonction dérivable ,

ta dérivée de g est fausse. Utilise plutôt la formule de dérivation ci-dessus.

Tu as utilisé implicitement la formule
qui est fausse

[Lmaths]

Très bien, alors en appliquant cette formule, je trouve :

g'(x) = 2*f(x)*f'(x) - 2
= 2*f(x) * 1/f(x) -2
= 2*f(x)/f(x) -2
= 2 - 2
= 0

Je pense qu'il s'agit de la bonne réponse ? Et pour ensuite en déduire l'expression de f(x) pour x réel positif, il faut isoler f(x) dans l'expression de g(x) ?

[mathelot]

oui, c'est correct. g' est la fonction nulle sur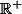

Que peut-on dire de g? que vaut g ? l'idée est de calculer d'abord g .

[mathelot]

Calculer g(0). En déduire la formule pour la fonction g puis l'expression de f.

[Lmaths]

Ah, d'accord j'ai compris. Donc vu que la dérivé de g est 0, alors g est constante et puisqu'on a la valeur de f(0) on fait g(0). Donc :

g(0) = f^2(0) - 2*0
= 1

Donc g(x) = 1, est-ce bien ça ?
Si on continue sur cette voie, cela donne que :

f^2(x) - 2x = 1
f(x) - 2x = 1
f(x) = 1 + 2x

Cela m'a l'air d'avoir du sens ?

[Lmaths]

Ou alors faisons-nous la racine carrée ensuite ?

f^2(x) - 2x = 1
f^2(x) = 1 + 2x
f(x) = √(1+2x)

[mathelot]

Ah, d'accord j'ai compris. Donc vu que la dérivé de g est 0, alors g est constante sur R+ et puisqu'on a la valeur de f(0) on fait g(0). Donc :

g(0) = f^2(0) - 2*0
= 1

Donc g(x) = 1, est-ce bien ça ? oui
Si on continue sur cette voie, cela donne que :

f^2(x) - 2x = 1
f^2(x) - 2x = 1
(f^2)(x) = 1 + 2x

Cela m'a l'air d'avoir du sens ?

Comme f garde un signe constant sur R+ et que f(0)=1 , f est donc positive sur R+ et
pour

[mathelot]

Ou alors faisons-nous la racine carrée ensuite ?

f^2(x) - 2x = 1
f^2(x) = 1 + 2x
f(x) = √(1+2x) définie sur R+

oui.

[Lmaths]

Très bien, je te remercie beaucoup de ton aide !

[Pisigma]

je poursuis mon idée







, seul le signe + convient





soit