Une suite récurrente
25 messages
- Page 1 sur 2 - 1, 2
Une suite récurrente
Bonjour,
J’ai bien séché sur cette question, je vous prie de me donner quelques indications :
U_1= 3/2
U_(n+1)= 1+ n/U_(n)
Trouver n tel que 2021<=U_(n)< 2022
Merci d’avance.
J’ai bien séché sur cette question, je vous prie de me donner quelques indications :
U_1= 3/2
U_(n+1)= 1+ n/U_(n)
Trouver n tel que 2021<=U_(n)< 2022
Merci d’avance.
Re: Une suite récurrente
Peux-tu préciser l'énoncé :
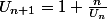
ou bien
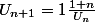
Rigoureusement, c'est la1ère interprétation.
Mais pour que l'exercice soit 'accessible', je parie plutôt pour la 2ème écriture.
ou bien
Rigoureusement, c'est la1ère interprétation.
Mais pour que l'exercice soit 'accessible', je parie plutôt pour la 2ème écriture.
Re: Une suite récurrente
En calculant les premiers termes, avec un tableur par exemple, on voit que la suite est strictement croissante, et que :
- le 1er terme supérieur à 3 arrive pour n=6=3*2
- le 1er terme supérieur à 4 arrive pour n=12=4*3
- le 1er terme supérieur à 5 arrive pour n=20=5*4
- le 1er terme supérieur à 6 arrive pour n=30=6*5
On peut donc conjecturer le comportement général. Ensuite, il faut le démontrer.
- le 1er terme supérieur à 3 arrive pour n=6=3*2
- le 1er terme supérieur à 4 arrive pour n=12=4*3
- le 1er terme supérieur à 5 arrive pour n=20=5*4
- le 1er terme supérieur à 6 arrive pour n=30=6*5
On peut donc conjecturer le comportement général. Ensuite, il faut le démontrer.
Re: Une suite récurrente
Alors il faut montrer que U(n(n+1))>n+1 pour tout n et ainsi U(2020. 2021)> 2021
Encore faut-il montrer aussi que U(2020.2021-1)> (2020.2021-1)/2021 pour que U(2020.2021)<2022 .
Sincèrement je ne vois toujours pas comment montrer tout ceci .
Encore faut-il montrer aussi que U(2020.2021-1)> (2020.2021-1)/2021 pour que U(2020.2021)<2022 .
Sincèrement je ne vois toujours pas comment montrer tout ceci .
Re: Une suite récurrente
on doit pouvoir montrer que \sqrt{1+4n}) puis utiliser cet encadrement pour répondre à ta question .
puis utiliser cet encadrement pour répondre à ta question .
Re: Une suite récurrente
tournesol a écrit:on doit pouvoir montrer quepuis utiliser cet encadrement pour répondre à ta question .
Ne serait-ce pas plutôt
Re: Une suite récurrente
L'exercice n'est pas simple du tout.
Si on manipule les données dans tous les sens, on finit par trouver des choses.
On pressent que U(n) atteint un nombre cible k lorsque n atteint k*(k-1)
Si on calcule W(n) =U(n)*(U(n)-1) on constate qu'on a une suite qui a l'air de tendre vers n+0.5
Et on a une vague alternance. On pourrait s'intéresser aux 2 suites extraites : uniquement les termes d'indices pairs, et uniquement les termes d'indices impairs. Ces 2 suites sont plus 'régulières' que la suite d'origine.
Et on a envie de montrer que si W(n) est entre n+0.5-1/n et n+0.5, alors W(n+2) aussi
Dans quel contexte as-tu trouvé cet exercice, ça peut aider à trouver la solution 'idéale'.
Si on manipule les données dans tous les sens, on finit par trouver des choses.
On pressent que U(n) atteint un nombre cible k lorsque n atteint k*(k-1)
Si on calcule W(n) =U(n)*(U(n)-1) on constate qu'on a une suite qui a l'air de tendre vers n+0.5
Et on a une vague alternance. On pourrait s'intéresser aux 2 suites extraites : uniquement les termes d'indices pairs, et uniquement les termes d'indices impairs. Ces 2 suites sont plus 'régulières' que la suite d'origine.
Et on a envie de montrer que si W(n) est entre n+0.5-1/n et n+0.5, alors W(n+2) aussi
Dans quel contexte as-tu trouvé cet exercice, ça peut aider à trouver la solution 'idéale'.
Re: Une suite récurrente
Salut,
On peut montrer par recurence que, pour tout ,
, 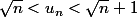 .
.
Pour l'hérédité, il suffit de montrer que :
1)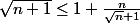 ce qui se vérifie facilement en retranchant 1 des deux côtés puis en multipliant les deux membres par
ce qui se vérifie facilement en retranchant 1 des deux côtés puis en multipliant les deux membres par 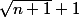 .
.
2)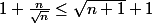 ce qui est évident.
ce qui est évident.
On peut montrer par recurence que, pour tout
Pour l'hérédité, il suffit de montrer que :
1)
2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une suite récurrente
Merci Ben 314.
Effectivement on arrive facilement à montrer que racine(n)< u(n)< racine(n)+1
Maintenant pour répondre à la question posée: si 2021<=u(n)< 2022 alors racine(n)<2022 et racine(n)+1> 2021 donc 2020^2< n < 2022^2
Mais est ce que la réciproque est vraie? Car on va trouver que 2020<u(n)< 2023 .
Si n=2021^2, bien sûr 2021<u(n)< 2022.
Est ce alors l’unique valeur possible pour n ?
Effectivement on arrive facilement à montrer que racine(n)< u(n)< racine(n)+1
Maintenant pour répondre à la question posée: si 2021<=u(n)< 2022 alors racine(n)<2022 et racine(n)+1> 2021 donc 2020^2< n < 2022^2
Mais est ce que la réciproque est vraie? Car on va trouver que 2020<u(n)< 2023 .
Si n=2021^2, bien sûr 2021<u(n)< 2022.
Est ce alors l’unique valeur possible pour n ?
Re: Une suite récurrente
Non, tres clairement ce n'est pas l'unique valeur : la suite croit à la même vitesse que racine(n) donc il y a un grand intervalle de valeurs de n pour lesquels Un est dans l'intervalle désiré. L'encadrement susmentionné permet de déterminer UN n qui marche et c'est tout. Mais d'un autre côté, l'énoncé tel qu'il est n'est pas clair du tout : faut il déterminer UN n qui marche ou bien TOUT les n qui marchent ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une suite récurrente
Je pense avoir bien mieux comme encadrement :
Si on suppose que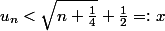 alors
alors 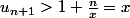 (car
(car 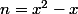 ) puis
) puis 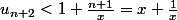 donc pour que la recurrence fonctionne, il suffit de verifier que
donc pour que la recurrence fonctionne, il suffit de verifier que +\frac14}+\frac12=\sqrt {x^2-x+\frac94}+\frac12) c'est à dire
c'est à dire ^2\leq x^2-x+\frac 94) ce qui est vrai (pile poil !!!!)
ce qui est vrai (pile poil !!!!)
Et comme l'inégalité supposée au depart est vraie pour n=1 et n=2, ça montre que, pour tout n, on a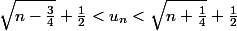
Ce qui, cette fois, est extrêmement précis pour n grand.
Si on suppose que
Et comme l'inégalité supposée au depart est vraie pour n=1 et n=2, ça montre que, pour tout n, on a
Ce qui, cette fois, est extrêmement précis pour n grand.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une suite récurrente
Bonjour
Juste une remarque
Le superbe encadrement trouvé par Ben permet de démontrer la conjecture de Lycéen95 qui disait en résumé :
C'est après n=p(p-1) que devient pour la première fois supérieur à p (p entier supérieur à 1)
devient pour la première fois supérieur à p (p entier supérieur à 1)
Donc si n=p(p-1) on a <p et
<p et  >p . On le démontre avec l'encadrement :
>p . On le démontre avec l'encadrement :
Soit n=p(p-1) on a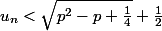 c'est à dire
c'est à dire 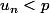
et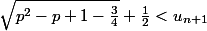 ou
ou 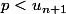
Donc devient supérieur à 2021 pour la première fois pour n=2020*2021+1
devient supérieur à 2021 pour la première fois pour n=2020*2021+1
et il le reste jusqu'à n=2021*2022 soit 4041 termes de la suite.
Juste une remarque
Le superbe encadrement trouvé par Ben permet de démontrer la conjecture de Lycéen95 qui disait en résumé :
C'est après n=p(p-1) que
Donc si n=p(p-1) on a
Soit n=p(p-1) on a
et
Donc
et il le reste jusqu'à n=2021*2022 soit 4041 termes de la suite.
Re: Une suite récurrente
En fait, bien que persuadé que le comportement est le même pour n'importe quel U1>0 (a savoir que Un-racine(n) tend vers 1/2), je n'arrive pas à le montrer proprement.
On peut aussi généraliser en prenant
U(n+1)=2k+n/U(n) avec U(1)>0 fixé
où k est une constante >0 : je ne pense pas que ça change grand chose à une éventuelle preuve mais ça risque de rendre les choses plus claires.
On peut aussi généraliser en prenant
U(n+1)=2k+n/U(n) avec U(1)>0 fixé
où k est une constante >0 : je ne pense pas que ça change grand chose à une éventuelle preuve mais ça risque de rendre les choses plus claires.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une suite récurrente
On peut au moins prouver facilement l'équivalence à 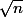 en utilisant l'hérédité de ton premier encadrement :
en utilisant l'hérédité de ton premier encadrement :
Les termes successifs sont des fonctions homoraphiques de , qui sont donc faciles à borner .
, qui sont donc faciles à borner .
On peut alors calculer que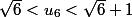
Les termes successifs sont des fonctions homoraphiques de
On peut alors calculer que
Re: Une suite récurrente
Bonjour Ben314
j'ai utilisé ton encadrement ici:
http://www.forum.math.ulg.ac.be/viewthr ... 9&id=61083
j'ai utilisé ton encadrement ici:
http://www.forum.math.ulg.ac.be/viewthr ... 9&id=61083
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
