Limite d'une fonction complexe

[marawita1]

Bonjour,

Je voudrais savoir comment calculer la limite en un point de la fonction si ou .

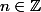
Par exemple si , quelles sont les limites suivantes :

1)


2)


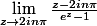
Merci d'avance.

[mathelot]

Bonjour,

Je voudrais savoir comment calculer la limite en un point de la fonction si ou .

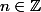
Par exemple si , quelles sont les limites suivantes :

1)


2)


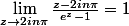
Merci d'avance.

[Black Jack]

Bonjour,

Je voudrais savoir comment calculer la limite en un point de la fonction si ou .

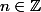
Par exemple si , quelles sont les limites suivantes :

1)


2)


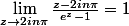
Merci d'avance.

Bonjour,

Pourquoi as-tu ajouté des valeurs absolues pour la question 1 ?
Cela enlève tout l'intérêt de la question.

[marawita1]

@mathelot, pourquoi vous avez ajouté le module dans le premier exemple? je veux savoir la limite sans ajouter

le module.

Si j'ai bien compris vous avez utilisé la dérivée dans l'exemple 2 (je n'ai pas fait attention à ça au début). Si on

change l'exemple , quelle est la limite de ?

[mathelot]

j'applique la définition suivante:

la limite de f(z) est infinie quand z tend vers :

tel que

avec est le disque ouvert de centre et de rayon r.

cette définition est basée sur les faits suivants:
Quand f(z) tend vers l'infini, aucune direction n'est privilégiée,
Pour obtenir la sphère (de Riemann), on ajoute au plan complexe un seul point à l'infini.

[marawita1]

J'ai trouvé dans des cours que n'a pas un sens dans le cas complexe

[mathelot]

J'ai trouvé dans des cours que n'a pas un sens dans le cas complexe

oui, tout à fait. C'est pour cette raison que l'on considère le module de l'image |f(z)|

[marawita1]

Si j'ai bien compris on ne peut pas définir la limite dans les deux exemples sans ajouter le module!!

[mathelot]

Oui

[marawita1]

ok merci beaucoup.

[Black Jack]

Bonjour,

Où est-il écrit que z est complexe pour l'exercice 1 ?

Même si z est souvent utilisé pour les complexes, ce n'est pas une obligation.

Sauf indication contraire, z peut-être réel ... et dans ce cas on n'a pas le droit d'ajouter les | |

La limite est alors différente si z --> n.Pi par valeurs inférieures ou par valeurs supérieures.

Il faudrait avoir un complément d'information de l'énoncé qui précise l'ensemble auquel appartient z.

[mathelot]

bonsoir,
le titre du fil est 'limite d'une fonction complexe"

[Black Jack]

bonsoir,
le titre du fil est 'limite d'une fonction complexe"

Bonjour,

Soit, mais le titre est écrit par le "poseur de question" qui dit lui-même ne pas bien connaître le sujet.
Et donc (comme c'est d'ailleurs très souvent le cas) le titre donné ne concerne pas forcément directement l'exercice qui a été proposé au cours.

Maintenant que ceci a été précisé, mataxita1 doit avoir compris que la limite (ex 1) ne peut pas se traiter de la même manière si z est dans C ou bien dans R...

Si pour l'ex 2, il est évident par l'énoncé que z est dans C, il n'en est pas de même pour l'ex 1.

[marawita1]

@Black Jack je cherche les limites pour complexe.

Si est réel, c’est évident pour moi.