Terminale! Le raisonnement par récurrence
14 messages
- Page 1 sur 1
Terminale! Le raisonnement par récurrence
bonjour ,
J'ai vraiment de difficultés avec cette exercice de math.
pourriez vous m'aidez s'il vous plait.
merci d'avance!
exercice:
Soit f la fonction définie sur J=[ 0;+∞[ par f(x)= 3- 1/X+1
a. Calculer f' la fonction dérivée de f et en déduire le sens de variations de f sur J.
b. On considère la suite ( Un) définie pour tout entier n par Un+1= f(un) et U0= 5. En utilisant le résultat de la question précédente, et en utilisant un raisonnement par récurrence, montrer que Un≥0 et déterminer le sens de variations de la suite (Un).
C. Démontrer que la suite (Un) converge
d. Déterminer la limite L de cette suite
J'ai vraiment de difficultés avec cette exercice de math.
pourriez vous m'aidez s'il vous plait.
merci d'avance!
exercice:
Soit f la fonction définie sur J=[ 0;+∞[ par f(x)= 3- 1/X+1
a. Calculer f' la fonction dérivée de f et en déduire le sens de variations de f sur J.
b. On considère la suite ( Un) définie pour tout entier n par Un+1= f(un) et U0= 5. En utilisant le résultat de la question précédente, et en utilisant un raisonnement par récurrence, montrer que Un≥0 et déterminer le sens de variations de la suite (Un).
C. Démontrer que la suite (Un) converge
d. Déterminer la limite L de cette suite
Re: Terminale! Le raisonnement par récurrence
Bonjour,
pour f(x) vous avez
1)= 3- \dfrac1X+1)
ou
2)= 3- \dfrac1{X+1})
Dites-nous ce que vous avez essayé, on n'est pas dans le jugement, ainsi on pourra vous aider.
pour f(x) vous avez
1)
ou
2)
Dites-nous ce que vous avez essayé, on n'est pas dans le jugement, ainsi on pourra vous aider.
Re: Terminale! Le raisonnement par récurrence
mathelot a écrit:Bonsoir,
il s'agit de?
Oui, mais quand je clique sur le lien rien n’apparaît
Re: Terminale! Le raisonnement par récurrence
phyelec a écrit:Bonjour,
pour f(x) vous avez
1)= 3- \dfrac1X+1)
ou
2)
Dites-nous ce que vous avez essayé, on n'est pas dans le jugement, ainsi on pourra vous aider.
j’avais fait la (a) est jai trouvé
f(x)= 3- 1/X+1 donc
f'(x)= 1/ (X+1)^2 >0
donc f est croissante.
il me reste alors la b,c et d a faire mais j'y arrive pas.
Re: Terminale! Le raisonnement par récurrence
Mel040404 a écrit:phyelec a écrit:Bonjour,
pour f(x) vous avez
1)= 3- \dfrac1X+1)
ou
2)
Dites-nous ce que vous avez essayé, on n'est pas dans le jugement, ainsi on pourra vous aider.
C’est la 2
j’avais fait la (a) est jai trouvé
f(x)= 3- 1/X+1 donc
f'(x)= 1/ (X+1)^2 >0
donc f est croissante.
il me reste alors la b,c et d a faire mais j'y arrive pas.
Re: Terminale! Le raisonnement par récurrence
si c'est la 2) votre calcul est juste et votre conclusion aussi.
Re: Terminale! Le raisonnement par récurrence
l'hypothèse de récurrence à l'ordre n :
calculez
une fois que vous fait cela que trouvez-vous, que pouvez vous dire du signe de ce que vous trouvez sachant que votre hypothèse de récurrence est
Re: Terminale! Le raisonnement par récurrence
on a:
=17/6)
d'où
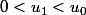
soit (H_n) l'hypothèse de récurrence:
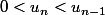
on compose par la fonction f qui est croissante sur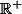
<f(u_n)<f(u_{n-1}))
...
d'où
soit (H_n) l'hypothèse de récurrence:
on compose par la fonction f qui est croissante sur
...
Modifié en dernier par mathelot le 23 Nov 2021, 00:45, modifié 2 fois.
Re: Terminale! Le raisonnement par récurrence
mathelot a écrit:on a:
d'où
soit (H_n) l'hypothèse de récurrence:
on compose par la fonction f qui est croissante sur
...
Merci, ça c pour la c?
Re: Terminale! Le raisonnement par récurrence
phyelec a écrit:est positif
l'hypothèse de récurrence à l'ordre n :est positif
calculez, mettez au même dénominateur
une fois que vous fait cela que trouvez-vous, que pouvez vous dire du signe de ce que vous trouvez sachant que votre hypothèse de récurrence estest positif
Merci ça c’est pour la b?
Re: Terminale! Le raisonnement par récurrence
Mel040404 a écrit:mathelot a écrit:on a:
d'où
soit (H_n) l'hypothèse de récurrence:
on compose par la fonction f qui est croissante sur
...
Merci, ça c pour la c?
non, c'est l'intégralité de la question (b). Il s'agit de démontrer par récurrence sur l'entier n,
que
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
