Suite

[VictorDnHaz]

Bonjour,

Savez-vous comment commencer cet exercice ?

Comment calculer la terme Un avec
U0=1 , U1=3 et U3=7
Un+3 =3Un+2 - 3Un+1 + Un
?
Si vous savez également comment écrire un programme python qui permette de calculer la valeur Un en prenant en entrée n, cela m'aiderez énormément.
Merci de votre aide.

[catamat]

Bonjour

Ne serait ce pas plutôt U2=7 ?

D'autre part calculer Un , est ce que vous voulez dire exprimer Un en fonction de n ?

[VictorDnHaz]

Bonjour

Ne serait ce pas plutôt U2=7 ?

D'autre part calculer Un , est ce que vous voulez dire exprimer Un en fonction de n ?

Oui c'est exactement ça, U2=7. Et il faut exprimer Un en fonction de n.
Je pense qu'il faut utiliser le fait que la suite soit arithmétique donc Un=U0 + nr, mais je ne vois pas comment il faut faire en partant de Un+3...

[mathelot]

Bonjour
Soit E l'ensemble des suites vérifiant l'égalité.
E est un espace vectoriel de dimension 3.
On cherche des éléments de E qui soient des suites géométriques, on pose u_n=q^n.
Quelle équation vérifie q? (q complexe)

[VictorDnHaz]

Oula ... Je n'ai jamais vu cette méthode. Je ne vois pas du tout comment faire.

[tournesol]

Et l'équation caractéristique , ça te parles ?revois ton cours .
Les solutions sont des trinômes en n de degré inférieurs ou égaux à 2 .

[catamat]

Par récurrence (forte) on peut démontrer que la suite de terme général Vn=Un+1-Un est arithmétique de raison 2

[mathelot]

Bonsoir,
soit E l'ensemble (l'espace vectoriel) des suites (u) vérifiant l'égalité de récurrence:


on veut montrer que E est de dimension 3

1) on cherche une suite (v) géométrique vérifiant l'égalité (*)
on pose pour n entier et q réel non nul.
Montrer que q vérifie l'équation
2) vérifier que les suites (a),(b),(c) définies par
vérifient l'égalité (*)
3)admis: les suites (a),(b),(c) forment une base de E
4) calculer les coordonnées de u dans la base (a,b,c)
En déduire la formule pour

[mathelot]

Bonsoir,
soit E l'ensemble (l'espace vectoriel) des suites (u) vérifiant l'égalité de récurrence:


On cherche les suites géométriques vérifiant l'égalité (*)
on pose pour n entier et q réel non nul.
Montrer que q vérifie l'équation

On a

La suite (v) vérifie:

[mathelot]

2) Pour tout n entier,



la suite (a) vérifie l'égalité (*):

1-3+3-1=0
donc la suite (a) appartient à E.


la suite (b) vérifie l'égalité (*):

pour tout n,
donc la suite (b) appartient à E.

la suite (c) vérifie l'égalité (*):

pour tout n,
donc la suite (c) appartient à E.

[mathelot]

Admis: les suites (a),(b),(c) forment une base de E

la suite (u) a donc des coordonnées x,y,z réelles dans cette base. On va calculer x,y et z.

[tournesol]

Bonsoir mathelot
En toute rigueur , , et .

[mathelot]

@tournesol : oui, tout à fait

[mathelot]

Calcul des coordonnées de la suite (u) dans la base (a;b;c):


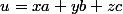
ce qui se traduit par



en particulier pour n=0


en particulier, pour


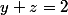
pour n=2


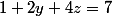
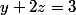
d'où
d'où
pour tout entier n:

[catamat]

Bon, j'avais évoqué une autre méthode possible à partir d'une suite arithmétique. Ok c'est loin d'être une méthode applicable dans tous les cas, mais ici elle fonctionne, je la développe donc :
Soit pour tout entier n,

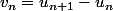
On souhaite démontrer que est arithmétique de raison 2 c'est à dire que pour tout entier n,

L'initialisation est rapide, démontrons l'hérédité
Supposons que pour un entier n on ait

Alors








Donc(v_n) est arithmétique de raison 2
Pour tout entier n,

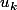On a car les différents , pour k compris entre 1 et n-1, s'éliminent

Donc

[mathelot]

Alors

il y a une erreur de signe

[catamat]

Merci Mathelot d'avoir lu attentivement !
J'ai corrigé l'erreur en question