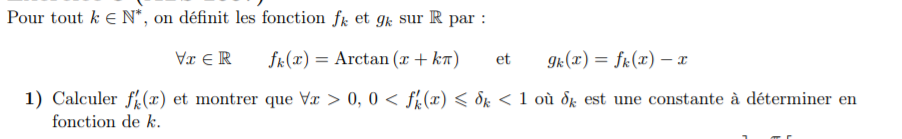Exercice sur les fonctions

[Andamir93]

Bonjour,

J'ai un exercice a faire et j'éprouve des difficulté à réaliser une partie de la première question qui est la suivante:



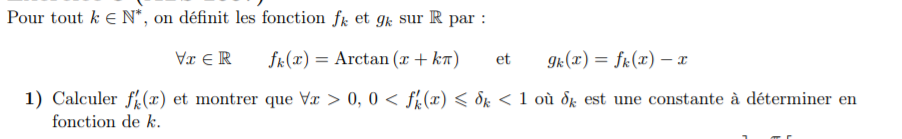
J'ai bien trouver la dérivée (selon moi): f(x)'=1/1+(x+kpi)^2 (Je ne sais pas comment écrire cela "proprement" sur le forum)

Pour prouver l'inégalité, j'ai compris qu'il fallait calculer delta k mais je n'ai aucune idée de comment faire cela.

Puis-je avoir des indications ?
Merci bien.

Cordialement,

[tournesol]

Ta dérivée est manifestement décroissante sur R+ , donc le max est facile à déterminer .

[phyelec]

Bonjour,
le truc à bien voir c'est que x est strictement positif sinon on ne pourrait écrire ce qui suit , donc pour x>0 :

[tournesol]

Bonsoir .
x peut très bien être nul puisque k appartient à N*

[Andamir93]

Je vous remercie pour vos réponses mais je ne comprend pas comment vous en venez à vos conclusion. J’aimerai « une méthode » si possible pour pouvoir répondre à des cas similaire si cela ce présente.

Merci bien.

[Andamir93]

Comment vous arriver à déterminer delta k ? Est simplement du raisonnement ? Ou un calcul s’impose ?

[tournesol]

As tu compris mon premier message ?

[Andamir93]

Ta dérivée est manifestement décroissante sur R+ , donc le max est facile à déterminer .

Si vous parler de celui ci, si j’ai bien compris vous avez fait une étude de fonction et je dois déterminer le maximum de celle ci ? Et la valeur sera delta k ?

Je suis censé trouver une fonction décroissante sur R+

[phyelec]

Bonjour,

suivez les conseils de Tournesol. Calculez la dérivée de f'(x), donc calculer f''(x) et regardez son signe.

rappel : Si une fonction est décroissante et dérivable sur un intervalle alors sa dérivée est négative sur cet intervalle.

[tournesol]

Aussi par composition :
(x+kpi)^2 est croissante sur R+ , donc 1+(x+kpi)^2 est croissante sur R+ , et donc son inverse est décroissante sur R+ .

[Andamir93]

Voici ce que j’ai trouver pour la dérivée mais cela me semble faux.


Je ne comprend pas pourquoi vous me demandez cela. Je pense aussi que je n’est pas compris la question du coup.

[phyelec]

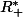
Pour trouver le maximum de f'(x) sur . Votre calcul est correcte.

[phyelec]

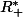
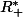
Vous pouvez étudiez le sens de variation de f''(x), vous verrez que f'(x) est décroissante sur l'intervalle , il faut trouver le maximum de f'(x) sur l'intervalle car votre question est posée pour x> 0

[tournesol]

x peut être nul puisque k appartient à N* et tout majorant sur R+ est majorant sur R+*

[Andamir93]

Bonsoir, je vous remercie pour l’aide que vous m’apporter.

Voici où j’en suis :

N’aurait t’il pas un moyen pour simplifier rapidement le dénominateur ? Car là je suis partir pour faire la double distributivité et je pense que je vais me perdre rapidement.

Cordialement,

[tournesol]

ta dérivée seconde est
Le dénominateur est supérieur ou égal à 1( =1+carré) donc strictement positif.
Ton numérateur est strictement positif sur R+ (2kpi+ positif) .
à cause du - , f"(x) est strictement négatif sur R+ .

[Andamir93]

Il ne manque pas un carré au dénominateur ? Et je suis pas censé trouver des valeurs de x pour quand le numéro et le dénominateur =0 et ensuite je calcul le maximum en remplacent les x dans la fonction ?

[phyelec]

oui, il manque un carré au dénominateur ( Latex a joué un tour à Tournesol).

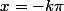
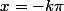
Pour votre calcul, vous trouvez que f''(x) s'annule pour , cela veut dire que f'(x) change de sens de croissance pour . Faites le tableau de variation et montrez le moi.

[Andamir93]

Voici le tableau de variation selon moi

[phyelec]

votre tableau est correcte. Donc vous voyez que :

1) f'(x) est croissante de - l'infini à -k
2) f'(x) est décroissante de -k à + l'infini donc de 0 à + l'infini (soit )
3) le maximum de f'(x) est 1.

sur l'intervalle [0, +oo [ on a f'(x) <1 ( car 1 est le maximum)
comme f'(x) est décroissante sur l'intervalle [0, +oo [ on a f'(x) f'(0) <1
f'(0)=