Endomorphismes

[jordvnsd]

Bonjour à tous

Dans le cadre d'un devoir je suis amené à étudier un endomorphisme d'un espace vectoriel E.

Soit u un endomorphisme de E. Soit u^n = u°u°u.....°u (avec n entier naturel)

Il m'est demandé de montrer que si la suite (u^n) est bornée alors toutes les valeurs propres de u sont module inférieur ou égal à 1.



j'ai démaré en traduisant le fait que u^ soit bornée et en obtenant des inégalités sur les normes mais je suis bloqué. une personne pourrais m'aider s'il vous plaît
Merci

[catamat]

Bonjour
Si x est un vecteur propre de valeur propre , on peut démontrer que , cela suffit pour conclure...

[jordvnsd]

merci
je suis parti de de ce que vous avez indiqué et j'ai utilisé le fait que u^n soit borné et donc majoré module de l^nx
ensuite j'ai conclu qu'il fallait nécessairement avoir que le module de la valeur propre soit inferieur ou égale à 1

est-ce maladroit?

[catamat]

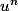
J'aurais plutôt utilisé la contrapposé, c'est à dire si le module de est strictement supérieur à 1 alors n'est pas bornée...

[jordvnsd]

merci j'ai montrer que la suite ne converge pas donc n'est pas bornée

j'aurais une dernière question ( si bien sûr vous êtes disponible)

soit Un = ( Id + u + u^2 + ....+u^n)*1/(n+1) un endomorphisme et id l'endo identité de E (espace vectoriel normé)
on suppose que 1 n'est pas valeur propre de u: Montrer que la suite (Un) converge

j'ai du mal à débuter

[GaBuZoMeu]

Tu supposes toujours que la suite est bornée, je pense ?

[jordvnsd]

oui tout à fait j'ai oublié de l'indiquer