Soit
 =f(a)f(b))
Comment à partir de cette égalité peut on démontrer que est une fonction exposant?
Re-bonjour,
Tout d'abord ce n'est pas simplement une égalité mais une identité c'est à dire
 \in R^2, f(a+b)=f(a)f(b))
Je me permets de changer de notation car a et b sont plutôt associés à des constantes
Démontrer que si
 \in R^2, f(x+y)=f(x)f(y))
:
équation (1), alors
)
est la fonction exponentielle de base a avec a positif strict .
Il faut donc démontrer qu'une fonction f vérifiant l'équation (1) vérifie certaines propriétés de la fonction exponentielle de base a
- f(0) = 1
- f(x) est strictement positif sur R
- f vérifie une certaine équation différentielle à établir et résoudre pour obtenir l'expression de f
1) montrons qu f(0) = 1 En évaluant f en y = 0 :
=f(x)f(0))
soit
 [f(0)-1] = 0)
Solutions :
-
 = 0)
il s'agit de la foncftion f identiquement nulle qui vérifie bien (1) mais qui n'est pas bien intéressante !
on l'écarte dans la suite de la démo.
- f(0) = 1
2) montrons que f est strictement positive sur RSupposons qu'il existe
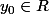
tel que
=0)
=f(x)f(y_0)=0)
pour tout

et donc pour tout
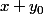
,
 = 0)
c'est la fonction identiquement nulle
donc en dehors de cette fonction il n'existe pas de fonction f qui s'annule sur R soit
 \in R^*)
pour
=f(u) = f^2(\frac{u}{2}))
donc f(u) >0
 \in R^{*+}) 3) équation différentielle vérifiée par f
3) équation différentielle vérifiée par fOn suppose que

est

=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\frac{f(x)f(h)-f(x)}{h}=f(x)\lim_{h \to 0}\frac{f(h)-1}{h}=f(x)\lim_{h \to 0}\frac{f(0+h)-f(0)}{h}=f(x)f'(0))

vérifie l'équation différentielle :
= f'(0) f(x))
= f'(0) f(x)\Leftrightarrow \frac{f'(x)}{f(x}= f'(0))
équivalence car
 \in R^{*+})
Solution:
)=xf'(0)+C)
=1 \rightarrow C = 0)
=e^{x f'(0)}= [e^{f'(0)}]^{x})
qui est bien de la forme
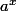
recherchée.